Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Arranging Ratios
We will learn how to solve different types of problems on arranging ratios in ascending order and descending order.
When a ratio is expressed in fraction or in decimal we first need to convert the ratio into whole number to compare the ratios.
The order of a ratio is important to compare two or more ratios. By reversing the antecedent and consequent of a ratio are different ratio is obtained.
Solved problems on comparing and arranging ratios in ascending and descending order:
1. Compare the ratios 113 : 115 and 1.6 : 1.2
Solution:
113 : 115 and 1.6 : 1.2
= 43 : 65 and 1610 : 1210
= 43 × 15 : 65 × 15 and 1610 × 10 : 1210 × 10
= 20 : 18 and 16 : 12
= 2018 and 1612
= 10×29×2 and 4×43×4
= 109 and 43
= 10 : 9 and 4 : 3
Now, 109 and 43 are to be compared. L.C.M. of 9 and 3 = 9
109 = 10×19×1 and 43 = 4×33×3
= 109 and 129
Since, 109 < 129
Therefore, 10 : 9 < 4 : 3
Hence, 113 : 115 < 1.6 : 1.2
2. Compare the ratios 14 : 23, 5 : 12 and 61 : 92 in
ascending order.
Solution:
Given ratios can be written as 1423, 512 and 6192
L.C.M. of the denominators 23, 12 and 92 = 276
1423 = 14×1223×12 = 168276
512 = 5×2312×23 = 115276
and
6192 = 61×392×3 = 183276
Since, 115276 < 168276 < 183276
Therefore, 512 < 1423 < 6192
Hence, 5 : 12 < 14 : 23 < 61 : 92
3. Arrange the ratios 1 : 3, 5 : 12, 4 : 15 and 2 : 3 in descending order.
Solution:
Given ratios can be written as 13, 512, 415 and 23
L.C.M. of the denominators 3, 12, 15 and 3 = 60
13 = 1×203×20 = 2060
512 = 5×512×5 = 2560
415 = 4×415×4 = 1660
and
23 = 2×203×20 = 4060
Since, 4060 > 2560 > 2060 > 1660
Therefore, 23 > 512 > 13 > 415
Hence, 2 : 3 > 5 : 12 > 1 : 3 > 4 : 15.
● Ratio and proportion
- Basic Concept of Ratios
- Important Properties of Ratios
- Ratio in Lowest Term
- Types of Ratios
- Comparing Ratios
- Arranging Ratios
- Dividing into a Given Ratio
- Divide a Number into Three Parts in a Given Ratio
- Dividing a Quantity into Three Parts in a Given Ratio
- Problems on Ratio
- Worksheet on Ratio in Lowest Term
- Worksheet on Types of Ratios
- Worksheet on Comparison on Ratios
- Worksheet on Ratio of Two or More Quantities
- Worksheet on Dividing a Quantity in a Given Ratio
- Word Problems on Ratio
- Proportion
- Definition of Continued Proportion
- Mean and Third Proportional
- Word Problems on Proportion
- Worksheet on Proportion and Continued Proportion
- Worksheet on Mean Proportional
- Properties of Ratio and Proportion
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
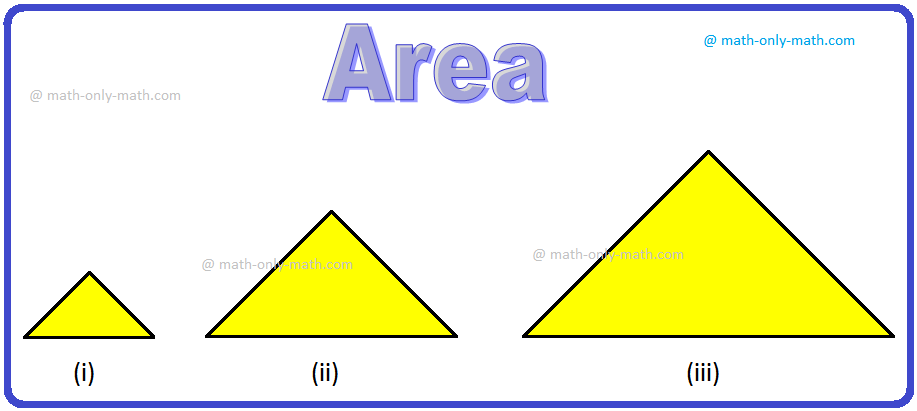
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
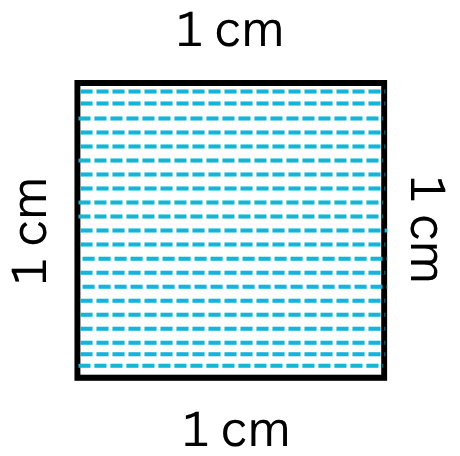
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
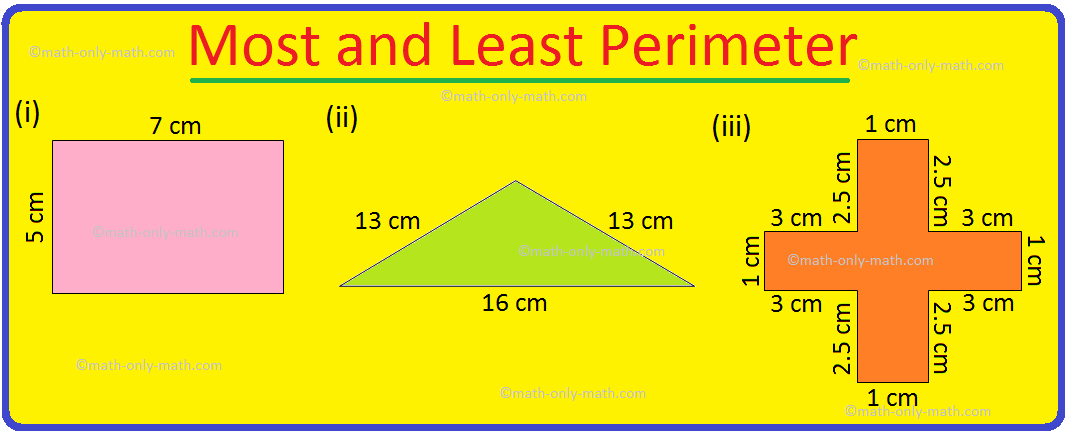
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
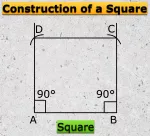
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
Perimeter of a Figure | Perimeter of a Simple Closed Figure | Examples
Jul 16, 25 02:33 AM
Perimeter of a figure is explained here. Perimeter is the total length of the boundary of a closed figure. The perimeter of a simple closed figure is the sum of the measures of line-segments which hav…

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.