Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Types of Fractions
The three types of fractions are :
Proper Fraction
Improper Fraction
Mixed Fraction
A fraction can be classified in three ways proper fraction, improper fraction and mixed fraction.
Let us discuss the three types of fractions with the help of an example.
If Sufi has 3 cookies and she wants to give equal share to Rachel, what share both will get? We divide 3 by 2. It is written as fraction \(\frac{3}{2}\).
In the above example of sharing 3 cookies among Sufi and Rachel the fraction \(\frac{3}{2}\) has 3 as numerator and 2 as denominator. When the numerator is greater than the denominator, the fraction is called the improper fraction. Thus an improper fraction represents a quantity greater than one.
We can represent the share of cookies received by Sufi and Rachel in the following way.
We can write this as 1 \(\frac{1}{2}\), which is a combination of a whole number and a fraction.
This is called a mixed fraction. Thus, an improper fraction can be expressed as a mixed fraction, where quotient represents the whole number, remainder becomes the numerator and divisor is the denominator. A fraction, where the numerator is less than the denominator is called the proper fraction for example, \(\frac{2}{3}\), \(\frac{5}{7}\), \(\frac{3}{5}\) are proper fractions. A fraction with numerator 1 is called a unit fraction.
Proper Fractions:
Fractions whose numerators are less than the denominators are called proper fractions. (Numerator < denominator)
For examples:
\(\frac{2}{3}\), \(\frac{3}{4}\), \(\frac{4}{5}\), \(\frac{5}{6}\), \(\frac{6}{7}\), \(\frac{2}{9}\) \(\frac{5}{8}\), \(\frac{2}{5}\), etc are proper fractions.
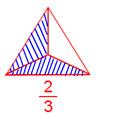
Two parts are shaded in the above diagram. Total number of equal parts is 3. Therefore, the shaded part can be represented as \(\frac{2}{3}\)
in fraction. The numerator (top number) is less compared to the
denominator (bottom number). This type of fraction is called proper
fraction.
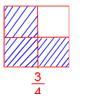
Similarly,
Three parts are shaded in the above diagram. Total number of equal parts is 4. Therefore, the shaded part can be represented as \(\frac{3}{4}\) in fraction. The numerator (top number) is less compared to the denominator (bottom number). This type of fraction is called proper fraction.
Note: The value of a proper fraction is always less than 1.
Definition of Proper Fraction: A fraction whose numerator is less than the denominator is called proper fraction.
A proper fraction is always less than a whole.
For example, \(\frac{3}{8}\), \(\frac{9}{11}\), \(\frac{18}{19}\), \(\frac{35}{99}\) etc. are proper fractions.
Improper Fractions:
Fractions with the numerator either equal to or greater than the denominator are called improper fraction. (Numerator = denominator or, Numerator > denominator)
Fractions like \(\frac{5}{4}\), \(\frac{17}{5}\), \(\frac{5}{2}\) etc. are not proper fractions. These are improper fractions. The fraction \(\frac{7}{7}\) is an improper fraction.
The fractions \(\frac{5}{4}\), \(\frac{3}{2}\), \(\frac{8}{3}\), \(\frac{6}{5}\), \(\frac{10}{3}\), \(\frac{13}{10}\), \(\frac{15}{4}\), \(\frac{9}{9}\), \(\frac{20}{13}\), \(\frac{12}{12}\), \(\frac{13}{11}\), \(\frac{14}{11}\), \(\frac{17}{17}\) are the examples of improper fractions. The top number (numerator) is
greater than the bottom number (denominator). Such type of fraction is
called improper fraction.
Notes:
(i) Every natural number can be written as a fraction in which 1 is it's denominator. For example, 2 = \(\frac{2}{1}\), 25 = \(\frac{25}{1}\), 53 = \(\frac{53}{1}\), etc. So every natural number is an improper fraction.
(ii) The value of an improper fraction is always equal to or greater than 1.
Definition of Improper Fraction: A fraction whose numerator is greater than the denominator is called an improper fraction.
An improper fraction is always greater than a whole.
For example, \(\frac{4}{3}\), \(\frac{7}{5}\), \(\frac{19}{9}\), \(\frac{8}{7}\) etc. are improper fractions.
Mixed Fractions:
A combination of a proper fraction and a whole number is called a mixed fraction.
1\(\frac{1}{3}\), 2\(\frac{1}{3}\), 3\(\frac{2}{5}\), 4\(\frac{2}{5}\), 11\(\frac{1}{10}\), 9\(\frac{13}{15}\) and 12\(\frac{3}{5}\) are examples of mixed fraction.
Two \(\frac{1}{2}\), make a whole.
What will you get if you add one more \(\frac{1}{2}\) to a whole?
Now, you have three half or you can say that you have a whole and a half or \(\frac{1}{2}\).
Number such as 1\(\frac{1}{2}\) is a mixed number.
In other words:
A fraction which contains of two parts: (i) a natural number and (ii) a proper fraction, is called a mixed fraction, e.g., 3\(\frac{2}{5}\), 7\(\frac{3}{4}\), etc.
In 3\(\frac{2}{5}\), 3 is the natural number part and \(\frac{2}{5}\) is the proper fraction part.
In Fact, 3\(\frac{2}{5}\) means 3 + \(\frac{2}{5}\).
Mixed Number (or Mixed Fraction)
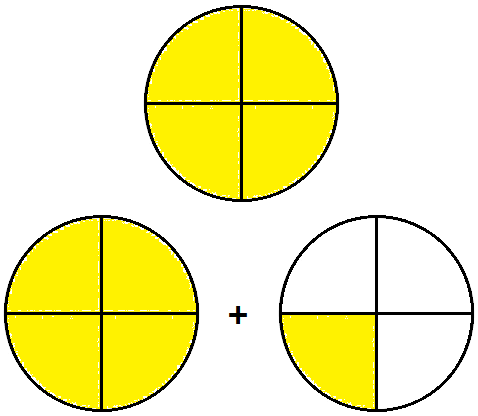
Here, a circle is divided into 4 equal parts. All the 4 parts are shaded.
Thus, the shaded part represents \(\frac{4}{4}\) or a whole or 1,
What do we get if we add a quarter more to \(\frac{4}{4}\)?
We get \(\frac{4}{4}\) + \(\frac{1}{4}\) = \(\frac{4 + 1}{4}\) = \(\frac{5}{4}\)
We also have 1 + \(\frac{1}{4}\) = \(\frac{5}{4}\)
We write, 1 + \(\frac{1}{4}\) as 1\(\frac{1}{4}\)
Thus, \(\frac{5}{4}\) = 1\(\frac{1}{4}\)
When an improper fraction is written as a combination of a whole number and a proper fraction, it is called a mixed number or mixed fraction.
Thus 2\(\frac{1}{5}\), 6\(\frac{1}{7}\), 4\(\frac{2}{3}\), 2\(\frac{1}{5}\), 2\(\frac{3}{4}\), etc. are mixed numbers.
Definition of Mixed Fractions: A fraction that is a combination of a whole number and a proper fraction is called a mixed fraction.
All improper fractions can be written in the form of mixed fractions.
Example: 2\(\frac{1}{4}\) is a mixed fraction, since 2 is whole number and \(\frac{1}{4}\) is a proper fraction.
Note: A mixed number is formed with a whole number and a fraction.
Properties of Mixed Fractions:
Property 1:
A mixed fraction may always be converted into an improper fraction.
Multiply the natural number by the denominator and add to the numerator. This new numerator over the denominator is the required fraction.
3\(\frac{1}{2}\) = \(\frac{3 × 2 + 1}{2}\) = \(\frac{6 + 1}{2}\) = \(\frac{7}{2}\) .
To know more Click Here.
Property 2:
An important fraction can be always be converted into a mixed fraction.
Divide the numerator by the denominator to get the quotient and remainder. Then the quotient is the natural number part and the remainder over the denominator is the proper fraction part of the required mixed fraction.
Example: \(\frac{43}{6}\) can be converted into a mixed fraction as follows:
7
6 |43
- 42
1
Dividing 43 by 6, we get quotient = 7 and remainder = 1.
Therefore, \(\frac{43}{6}\) = 7 \(\frac{1}{6}\)
To know more Click Here.
Note: Proper fraction is between 0 to 1. Improper fraction is 1 or greater than 1. Mixed fraction is grater than 1.
1. Write \(\frac{37}{4}\) as mixed fraction.
Solution:
So, Quotient = 9, Remainder = 1 and Divisor = 4
Mixed fraction = Quotient \(\frac{Remainder}{Divisor}\)
So, \(\frac{37}{4}\) can be expressed as 9\(\frac{1}{4}\) where 9 is a whole number and \(\frac{1}{4}\) is a proper fraction.
2. Classify the following as proper fractions, improper fractions or unit fractions.
\(\frac{8}{12}\), \(\frac{10}{27}\), \(\frac{17}{12}\), \(\frac{2}{5}\), \(\frac{1}{13}\), \(\frac{5}{12}\), \(\frac{6}{15}\), \(\frac{1}{32}\), \(\frac{31}{12}\), \(\frac{27}{4}\)
Solution:
3. Observe the following sets of fractions:
\(\frac{5}{11}\), \(\frac{3}{7}\), \(\frac{1}{9}\), \(\frac{6}{13}\), \(\frac{11}{15}\) .... (A) \(\frac{11}{8}\), \(\frac{7}{5}\), \(\frac{23}{11}\), \(\frac{15}{13}\), \(\frac{19}{14}\) .... (B)
In what respect, are the two sets different?
In the first set, the numerator of each fraction is less than the denominator.
We call such type of fractions as proper fractions.
In the second set, the numerator of each fraction is either greater than or equal to the denominator. We call such type of fractions as improper fractions.
Like Fractions:
Fractions with the same denominator are called like fractions.
For example: \(\frac{1}{9}\), \(\frac{2}{9}\), \(\frac{3}{9}\), \(\frac{5}{9}\) and \(\frac{7}{9}\) are like fractions.
Definition of Like Fractions: Fractions having the same denominators are called like fractions.
For example, \(\frac{1}{7}\), \(\frac{3}{7}\), \(\frac{2}{7}\), \(\frac{6}{7}\) are like fractions.
Unlike Fractions:
Fractions with the different denominators are called unlike fractions.
For example: \(\frac{4}{7}\), \(\frac{2}{9}\), \(\frac{5}{11}\), \(\frac{2}{5}\) and \(\frac{3}{4}\) are unlike fractions.
Definition of Unlike Fractions: Fractions having different denominators are called unlike fractions.
For example, \(\frac{3}{5}\), \(\frac{4}{7}\), \(\frac{5}{8}\), \(\frac{4}{9}\) etc. are unlike fractions.
Unit Fractions:
Fractions having 1 as numerator are called unit fractions.
For example, \(\frac{1}{6}\), \(\frac{1}{9}\), \(\frac{1}{12}\), \(\frac{1}{17}\) and \(\frac{1}{25}\) are unit fractions.
Definition of Unit Fractions:
A fraction having numerator 1 is called unit fraction.
For example, \(\frac{1}{2}\), \(\frac{1}{5}\), \(\frac{1}{18}\), \(\frac{1}{23}\), \(\frac{1}{50}\), \(\frac{1}{100}\) etc. are unit fractions.
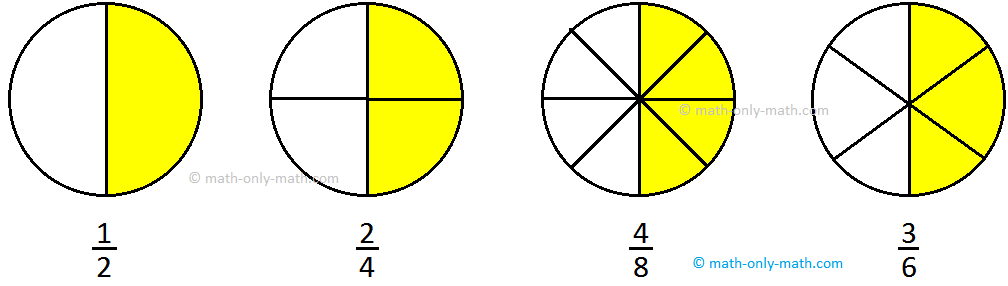
Equivalent Fractions:
Two or more fractions representing the same part (value) of the whole are called equivalent fractions.
In the given figure, \(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{3}{6}\) and \(\frac{4}{8}\) are equivalent fractions.
● We can obtain equivalent fraction of a given fraction by multiplying the numerator denominator by the same number (except zero).
For Example:
\(\frac{3}{5}\) = \(\frac{3 × 2}{5 × 2}\) = \(\frac{3 × 3}{5 × 3}\) = \(\frac{3 × 4}{5 × 4}\) = \(\frac{3 × 5}{5 × 5}\)
\(\frac{3}{5}\) = \(\frac{6}{10}\) = \(\frac{9}{15}\) = \(\frac{12}{20}\) = \(\frac{15}{25}\)
● We can obtain an equivalent fraction of a given fraction by dividing its numerator and denominator by their common factor (other than 1), if any.
For Example:
\(\frac{6}{10}\) = \(\frac{6 ÷ 2}{10 ÷ 2}\) = \(\frac{3}{5}\)
\(\frac{4}{8}\) = \(\frac{4 ÷ 4}{8 ÷ 4}\) = \(\frac{1}{2}\)
Hence, we can generate equivalent fractions of any given fraction by:
☞ Multiplying its numerator and denominator by the same number (other than 0) or,
☞ Dividing its numerator and denominator by their common factor (other than 1), if any.
For Example:
1. Replace 🔲 by the correct numeral.
(i) \(\frac{3}{5}\) = \(\frac{12}{🔲}\)
(ii) \(\frac{12}{18}\) = \(\frac{🔲}{3}\)
Solution:
(i) We observe the numerators.
Since. 12 = 3 × 4, so we multiply both the numerator and the denominator \(\frac{3}{5}\) of by 4.
\(\frac{3}{5}\) = \(\frac{3 × 4}{5 × 4}\) = \(\frac{12}{20}\)
Thus, replacing 🔲 by 20, we get \(\frac{3}{5}\) = \(\frac{12}{20}\)
(ii) We observe the denominators.
Since, 3 = 18 ÷ 6 so we divide both the numerator and the denominator of \(\frac{12}{18}\) by 6.
\(\frac{12}{18}\) = \(\frac{12 ÷ 6}{18 ÷ 6}\) = \(\frac{2}{3}\)
Hence, replacing 🔲 by 2, we get \(\frac{12}{18}\) = \(\frac{2}{3}\)
2. (i) Find an equivalent fraction of \(\frac{5}{11}\) whose numerator is 35.
(ii) Find an equivalent fraction of \(\frac{5}{9}\) whose denominator is 45.
Solution:
(i) Since 35 = 5 × 7 , so we multiply both the numerator and the denominate \(\frac{5}{11}\) by 7.
Hence, \(\frac{5}{11}\) = \(\frac{5 × 7}{11 × 7}\) = \(\frac{35}{77}\)
\(\frac{35}{77}\) is the required fraction.
(ii) Since, 45 = 9 × 5 so we multiply both the numerator and the denominator of \(\frac{5}{9}\) by 5.
\(\frac{5}{9}\) = \(\frac{5 × 5}{9 × 5}\) = \(\frac{25}{45}\)
Hence \(\frac{25}{45}\) the required fraction.
● Fraction
- Representations of Fractions on a Number Line
- Fraction as Division
- Types of Fractions
- Conversion of Mixed Fractions into Improper Fractions
- Conversion of Improper Fractions into Mixed Fractions
- Equivalent Fractions
- Interesting Fact about Equivalent Fractions
- Fractions in Lowest Terms
- Like and Unlike Fractions
- Comparing Like Fractions
- Comparing Unlike Fractions
- Addition and Subtraction of Like Fractions
- Addition and Subtraction of Unlike Fractions
- Inserting a Fraction between Two Given Fractions
Numbers Page
6th Grade Page
From Types of Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

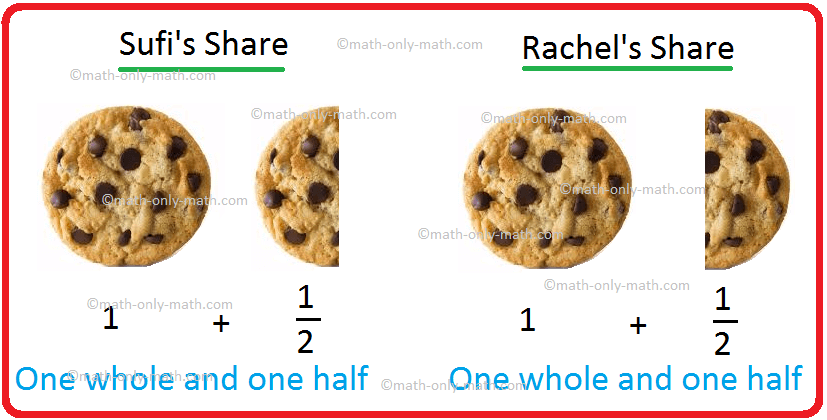


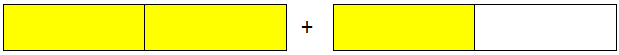



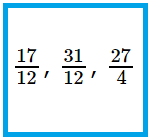
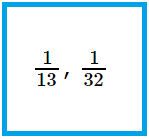
![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)











New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.