Subscribe to our YouTube channel for the latest videos, updates, and tips.
Worksheet on Quadrilateral
In worksheet on quadrilateral we will solve 10 different types of question in quadrilateral.
1. A quadrilateral has ………….. angles, …………… diagonals, ……………… sides and ………… vertices.
2. In a quadrilateral, ∠A = ∠B = 75° and ∠D = 110°, find ∠C.
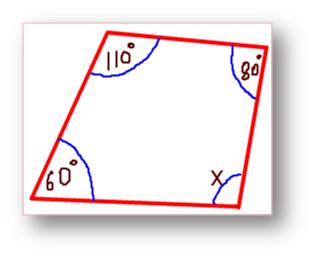
3. Find the unknown angle in the quadrilateral;
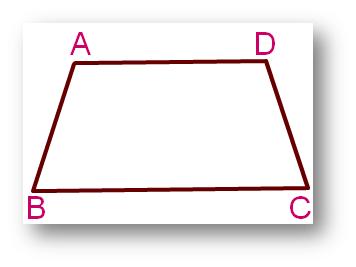
4. Which of the sides appear to be parallel? Write them using the symbol:
(i)
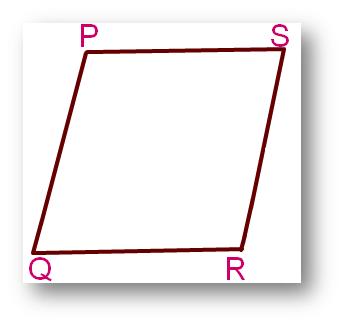
(ii)
5. LMNO is a Parallelogram.
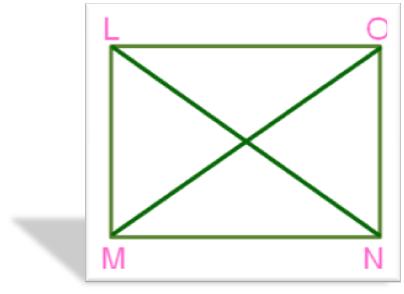
Fill in the Blanks:
(a) ∠M = ………………….
(b) ML = …………….
(c) MN = …………….
(d) ∠L = ………………….
(e) Two diagonals equals ……………….. and ……………..
6. A rhombus has all its …………… equal.
7. Opposite angles of a rhombus are ……………….
8. Draw a rhombus whose one side is 5 cm and one angle is 60°
9. Draw a parallelogram ABCD with its sides 5 cm and 7 cm and A is 75°.
10. A quadrilateral has three angles equal to 75°, 75° and 110°. Find its unknown angle.
Construction of Perpendicular Lines by using a Protractor.
Sum of Angles of a Quadrilateral.
Practice Test on Quadrilaterals.
5th Grade Geometry Page
5th Grade Math Worksheets
5th Grade Math Problems
From Worksheet on Quadrilateral to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Average | Word Problem on Average | Questions on Average
May 19, 25 02:53 PM
In worksheet on average we will solve different types of questions on the concept of average, calculating the average of the given quantities and application of average in different problems. -
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.