Subscribe to our YouTube channel for the latest videos, updates, and tips.
To find Highest Common Factor by using Prime Factorization Method
To find highest common factor by using prime factorization method is discussed here.
Step I:
Find the prime factorization of each of the given numbers.
Step II:
The product of all common prime factors is the HCF of the given numbers.
Let us consider some of the examples to find highest common factor by using prime factorization method.
1. Find highest common factor (HCF) of 14 and 8 by using prime factorization method.
Solution:
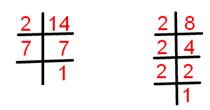
14 = 1 × 2 × 7.
8 = 1 × 2 × 2 × 2.
Common factor of 8 and 14 = 1 and 2.
H.C.F. is the product of lowest powers of factors common to all numbers.
Highest common factor of 8 and 14 = 2.
2. Find highest common factor (HCF) of 9 and 27 by using prime factorization method.
Solution:
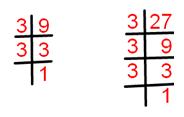
9 = 1 × 3 × 3.
27 = 1 × 3 × 3 × 3.
Common factor of 9 and 27 = 1, 3 and 3.
Highest common factor of 9 and 27 = 3 × 3 = 9.
3. Find highest common factor (HCF) of 6 and 16 by using prime factorization method.
Solution:
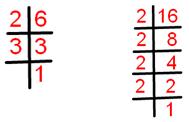
6 = 1 × 2 × 3.
16 = 1 × 2 × 2 × 2 × 2.
Common factor of 6 and 16 = 2.
Highest common factor of 6 and 16 = 2.
4. Find highest common factor (HCF) of 18 and 24 by using prime factorization method.
Solution:
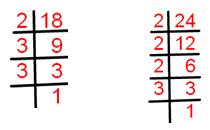
18 = 1 × 2 × 3 × 3.
24 = 1 × 2 × 2 × 2 × 3.
Common factor of 18 and 24 = 1, 2, 3.
Highest common factor of 18 and 24 = 2 × 3 = 6.
5. Find highest common factor (HCF) of 12 and 56 by using prime factorization method.
Solution:
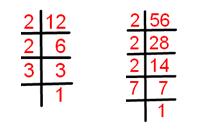
12 = 1 × 2 × 2 × 3.
56 = 1 × 2 × 2 × 2 × 7.
Common factor of 12 and 56 = 1, 2, 2.
Highest common factor of 12 and 56 = 2 × 2 = 4.
6. Find the HCF of 108 and 132 by prime factorization method.
Solution:
108 = 2 × 2 × 3 × 3 × 3
132 = 2 × 2 × 3 × 11
Thus, the HCF is 2 × 2 × 3 = 12
● Factors.
● Highest Common Factor (H.C.F).
● Examples on Highest Common Factor (H.C.F).
● Greatest Common Factor (G.C.F).
● Examples of Greatest Common Factor (G.C.F).
● To find Highest Common Factor by using Prime Factorization Method.
● Examples to find Highest Common Factor by using Prime Factorization Method.
● To find Highest Common Factor by using Division Method.
● Examples to find Highest Common Factor of two numbers by using Division Method.
● To find the Highest Common Factor of three numbers by using Division Method.
5th Grade Numbers Page
5th Grade Math Problems
From To find Highest Common Factor by using Prime Factorization Method to HOMEPAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
How to Find the Average? | What Does Average Mean? | Definition
May 15, 25 06:05 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Worksheet on Rounding Off Number | Rounding off Number | Nearest 10
May 15, 25 05:12 PM
In worksheet on rounding off number we will solve 10 different types of problems. 1. Round off to nearest 10 each of the following numbers: (a) 14 (b) 57 (c) 61 (d) 819 (e) 7729 2. Round off to -
Worksheet on Rounding Decimals | Questions Related to Round a Decimal
May 15, 25 11:52 AM
The worksheet on rounding decimals would be really good for the students to practice huge number of questions related to round a decimal. This worksheet include questions related -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 14, 25 03:01 PM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate -
Rounding Off to the Nearest Whole Number | Nearest 10, 100, and 1000
May 13, 25 03:43 PM
Here we will learn how to rounding off to the nearest whole number?
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.