To find Highest Common Factor by using Division Method

To find highest common factor by using division method is discussed here.

Finding highest common factor (H.C.F) by prime factorization for large number is not very convenient. The method of long division is more useful for large numbers. 

In this method we first divide the greater number by the smaller number. The remainder becomes the new divisor and the previous divisor as the new dividend. We continue the process until we get 0 remainder.

We use the repeated division method for finding highest common factor (H.C.F) of two or more numbers. 

To find highest common factor by using division method we follow these steps: 

Step I: 

Divide the large number by the smaller one. 

Step II: 

Then the remainder is treated as divisor and the divisor as dividend.

Step III: 

Divide the first divisor by the first remainder.


Step IV:

Divide the second divisor by the second remainder.


Step V:

Continue this process till the remainder becomes 0.


Step VI:

The divisor which does not leave a remainder is the H.C.F. or G.C.D. of the two numbers and thus, the last divisor is the required highest common factor (H.C.F) of the given numbers.


Let us consider some of the examples to find highest common factor (H.C.F) by using division method.

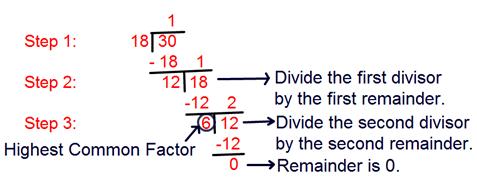
1. Find highest common factor (H.C.F) of 18 and 30 by using division method.

Solution:

Step I: 

Here we need to divide 30 by 18. 

[Divide the larger number by the smaller one]. 

Step II:

The first divisor is 18 and the remainder is 12, so we need to divide 18 by 12.

[Divide the first divisor by the first remainder].



Step III:

Now divide the second divisor 12 by the second remainder 6.

[Divide the second divisor by the second remainder].



Step IV:

The remainder becomes 0.



Step V:

Therefore, highest common factor = 6.

[The last divisor is the required highest common factor (H.C.F) of the given numbers].



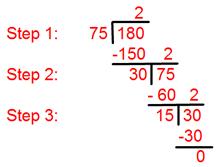
2. Find highest common factor (H.C.F) of 75 and 180 by using division method.

Solution:

Step I:

Here we need to divide 180 by 75.

[Divide the larger number by the smaller one].



Step II:

The first divisor is 75 and the remainder is 30, so we need to divide 75 by 30.

[Divide the first divisor by the first remainder].



Step III:

Now divide the second divisor 30 by the second remainder 15.

[Divide the second divisor by the second remainder].



Step IV:

The remainder becomes 0.



Step V:

Therefore, highest common factor = 15.

[The last divisor is the required highest common factor (H.C.F) of the given numbers].

1. Find the HCF of 112 and 144 by long division method.

Solution:

Divide 144 by 112

Divide 112 by remainder 32

Divide 32 by remainder 16

Now, remainder is 0

Hence, HCF of 112 and 144 is 16

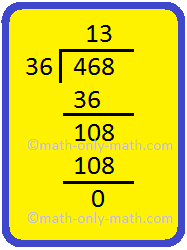
2. Find the HCF of 216, 468 and 828 by division method.

Solution:

Step 1: We will first find HCF of 216 and 828

Step 2: Now find HCF of 36 and 468.

Hence, HCF of 216, 468 and 828 is 36

HCF by Long Division Method:

In HCF by long division method we first divide the greater number by the smallest number and then divide the smaller number by the remainder. We continue the process until we get 0 remainder.

The divisor is the HCF of the given numbers.

For example:

Find the HCF of 318 and 504 by long division method.

Divide 504 by 318. Divide 318 by remainder 186. Divide 186 by remainder 132. Divide 132 by remainder 54. Divide 54 by remainder 24. Divide 24 by remainder 6. Now, remainder is 0. So, we cannot divide further.

Hence, 6 is the HCF of 318 and 514.

● Factors.

● Common Factors.

● Prime Factor.

● Repeated Prime Factors.

● Highest Common Factor (H.C.F).

● Examples on Highest Common Factor (H.C.F).

● Greatest Common Factor (G.C.F).

● Examples of Greatest Common Factor (G.C.F).

● Prime Factorisation.

● To find Highest Common Factor by using Prime Factorization Method.

● Examples to find Highest Common Factor by using Prime Factorization Method.

● To find Highest Common Factor by using Division Method.

● Examples to find Highest Common Factor of two numbers by using Division Method.

● To find the Highest Common Factor of three numbers by using Division Method.

5th Grade Numbers Page

5th Grade Math Problems

From To find Highest Common Factor by using Division Method to HOME PAGE