Subtraction of Polynomials
Subtraction of polynomials can be solved in two methods.
Follow the following steps to solve in the first method:
(i) Enclose the part of the expression to be subtracted in parentheses with a negative (-) sign prefixed
(ii) Remove the parentheses by changing the sign of each term of the polynomial expression which is in the parentheses.
(iii) Arrange the like terms.
(iv) Finally add the like terms to find the required subtraction.
For example:
1. Subtract: 2x - 5y + 3z from 5x + 9y - 2z.
First we need to enclose the first part which is to be subtracted in parentheses with a negative (-) sign prefixed.
5x + 9y - 2z – (2x - 5y + 3z)
Now we need to remove the parentheses by changing the sign of each term which is in the parentheses.
= 5x + 9y - 2z – 2x + 5y - 3z
= 5x – 2x + 9y + 5y - 2z - 3z, by arranging the like terms.
= 3x + 14y - 5z
First we need to enclose the first part which is to be subtracted in parentheses with a negative (-) sign prefixed.
x2 - y3 + z – (-6x2 - 8y3 + 15z)
Now we need to remove the parentheses by changing the sign of each term which is in the parentheses.
= x2 - y3 + z + 6x2 + 8y3 - 15z
= x2 + 6x2 - y3 + 8y3 + z - 15z, by arranging the like terms.
= 7x2 + 7y3 - 14z
Follow the following steps to solve the subtraction of polynomials in the second method:
Re-write the given expressions in two lines such that the lower line is the expression to be subtracted and like terms of both the expressions are one below the other.
Change the sign of each term in the lower line i.e. change the sign of each term of the expression to be subtracted.
Combine the terms column-wise with new signs assigned to the terms of lower line.
For example:
1. Subtract: x – 4y – 2z from 7x – 3y + 6z
First we will arrange the expressions in two lines such that the lower line of the expression is to be subtracted from the other, placing the like terms in the same column one below the other.
 |
Now by changing the sign (positive becomes negative and negative becomes positive) of each term in the lower line i.e. change the sign of each term of the expression to be subtracted (x – 4y – 2z). |
Therefore, the required answer is 6x + y + 8z.
First we will arrange the expressions in two lines such that the lower line of the expression is to be subtracted from the other, placing the like terms in the same column one below the other.
 |
Now by changing the sign (positive becomes negative and negative becomes positive) of each term in the lower line i.e. change the sign of each term of the expression to be subtracted (3a3 + 5a2 – 7a + 10). |
Thus, we have learnt how to solve subtraction of polynomials in both the methods.
● Terms of an Algebraic Expression
Types of Algebraic Expressions
Multiplication of Two Monomials
Multiplication of Polynomial by Monomial
Multiplication of two Binomials
From Subtraction of Polynomials to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 11, 24 09:08 AM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver… -
Points and Line Segment | Two Points in a Curved Surface | Curve Line
Dec 09, 24 01:08 AM
We will discuss here about points and line segment. We know when two lines meet we get a point. When two points on a plane surface are joined, a straight line segment is obtained. -
Solid Shapes | Basic Geometric Shapes | Common Solid Figures | Plane
Dec 08, 24 11:19 PM
We will discuss about basic solid shapes. We see a variety of solid objects in our surroundings. Solid objects have one or more shapes like the following. Match the objects with similar shape. -
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
Dec 07, 24 03:38 PM
2nd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students.
● Terms of an Algebraic Expression - Worksheet
Worksheet on Types of Algebraic Expressions
Worksheet on Degree of a Polynomial
Worksheet on Addition of Polynomials
Worksheet on Subtraction of Polynomials
Worksheet on Addition and Subtraction of Polynomials
Worksheet on Adding and Subtracting Polynomials
Worksheet on Multiplying Monomials
Worksheet on Multiplying Monomial and Binomial
Worksheet on Multiplying Monomial and Polynomial
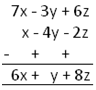
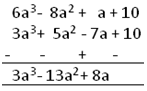
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.