Prime and Composite Numbers

What are the prime and composite numbers?

Prime Numbers:

Prime numbers are those numbers which have only two factors 1 and the number itself. 

In other words, a number which is divisible by only itself and 1 is a prime number. So, prime number has only two different factors 1 and the number itself.

For example, these numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, etc which have only two factors i.e. 1 and the number itself.

REMEMBER

1 is not considered as a prime number, why?

Because it does not have distinct two factors (i.e., 1 and the number itself are the same)

Observe the following:

All the factors of 2 are 1 and 2.

All the factors of 3 are 1 and 3.

All the factors of 4 are 1, 2 and 4.

All the factors of 5 are 1 and 5.

All the factors of 6 are 1, 2, 3 and 6.

We see that 2, 3 and 5 have only two factors namely 1 and the number itself. We call these numbers are prime numbers.

Hence the numbers having exactly two different factors, namely 1 and itself, are known as prime numbers.

2,3, 5, 7, 11, 13, 17, 19, ... are prime numbers.

Working Rules to Find the Prime Number.

Step I: Consider any number, i.e., 'n'.

Step II: Find out the factors of 'n'.

Step III: If 'n' has only two factors i.e., 1 and itself, then 'n' is a prime number.

Solved Examples on Prime Numbers:

1. Which of the following is a prime number?

(a) 23

(b) 18

(c) 25

(d) 15

Solution:

(a) 23 = 1 × 23

Hence, 23 is a prime number.

(b) Since 18 = 1 × 18 or 6 × 3

Hence, 18 is not a prime number.

(c) Since 25 = 1 × 25 or 5 × 5

Hence, 25 is not a prime number.

(d) Since 15 = 1 × 15 or 3 × 5

Hence, 15 is not a prime number.

So, the option (a) is correct.

2. The numbers 13 and 31 are prime numbers. Both these numbers have the same digits 1 and 3. Find such pairs of prime numbers up to 100.

Solution:

17 and 71, 37 and 73, 79 and 97 are the required pairs of prime numbers up to 100.

Twin Primes:

If the difference between the two prime numbers is 2 they are called twin primes.

or

Pairs of prime numbers having a difference of 2 are called twin primes.

For example, (3, 5), (5, 7) and (11, 13) are set of twin primes.

So, two consecutive prime numbers having only one number between them are called twin primes.

Definition of Twin Primes:

If two prime numbers can be paired with a difference of 2, that is they have one composite number between them, then the pair is called a twin prime.

For example, (3, 5), (5, 7), (11, 13), (17, 19), (41, 43), (59, 61), (71, 73), etc.

Solved Example on Twin Primes Numbers:

1. Write three pairs of prime numbers whose difference is 2, i.e., twin primes.

Solution:

We may write (3,5), (5,7) and (11, 13) as the required twin primes.

Co-Prime Numbers:

If two numbers have only 1 as a common factor, they are called as co-primes.

or

Two numbers are said to be co-prime, if they do not have a common factor other than 1.

For example, (2, 3), (4, 5), (3, 7) and (4, 9) are co-primes.

REMEMBER

● Two prime numbers are always co-prime.

● Two co-primes may or may not be both prime numbers, for example 4 and 9.

Solved Example on Co-Prime Numbers:

1. Which of the following are co-primes?

(i) 8, 10

(ii) 9, 10

(iii) 6, 8

(iv) 15, 18

Solution:

(i) 8 = 1 × 2 × 2 × 2

   10 = 1 × 2 × 5

2 is a common factor other than 1.

(ii) 9 = 1 × 3 × 3

    10 = 1 × 2 × 5

No common factor other than 1.

(iii) 6 = 1 × 2 × 3

      8 = 1 × 2 × 2 × 2

2 is a common factor other than 1.

(iv) 15 = 1 × 3 × 5

      18 = 1 × 3 × 3 × 2

3 is a common factor other than 1.

Hence, (9, 10) are co-primes.

Therefore, the option (ii) is correct.

2. Find four pairs of co-prime numbers.

Solution:

We may find any pair of co-prime numbers which do not have a common factor except 1.

Thus, (3, 5), (4, 9), (7, 10) and (31, 65) are four such pairs of co-prime numbers.

Composite Numbers:

Composite numbers are those numbers which have more than two factors.

In other words, a number that has more than two different factors is a composite number. So, a composite number is also exactly divisible by numbers other than 1 and itself.

For example, 4 is a composite number and it can be divided by 1, 2 and 4.

6 is a composite number and it can be divided by 1, 2, 3 and 6.

8 is a composite number and it can be divided by 1, 2, 4 and 8.  

9 is a composite number and it can be divided by 1, 3 and 9.

Therefore, 1 is a unique number that is neither prime nor composite as it has only one factor.

Observe the following:

All the factors of 4 are 1, 2, 4.

All the factors of 6 are 1, 2, 3, 6.

All the factors of 8 are 1, 2, 4, 8.

All the factors of 9 are 1, 3, 9.

We see that 4, 6, 8 and 9 have more than two factors.

We call these numbers as composite numbers.

Hence, the numbers having more than two different factors are known as composite numbers.

REMEMBER

(a) 1 is neither prime nor composite.

(b) 2 is a prime as well as an even number.

Working Rules to Find the Composite Number:

Step I: Consider the number, say 'p'.

Step II: Find out all the factors of 'p'.

Step III: If 'p' has more than two factors, then it is a composite number.

NOTE: The numbers 0 and 1 are neither prime nor composite numbers.

Observe the following table.

The numbers 2, 3, 5, ....... have only 2 factors, 1 and itself.

       Such numbers are called Prime numbers.

The numbers 4, 6, ...... have more than 2 factors.

      Such numbers are called Composite numbers.

Note:

(i) 1 is neither a prime nor a composite number.

(ii) 2 is the smallest prime number.

(iii) 2 is the only even prime number.

(iv) No prime number ends with zero or 5.

A prime number is a natural number which has only two different factors, 1 and the number itself. A composite number is a natural number which has more than two different factors.

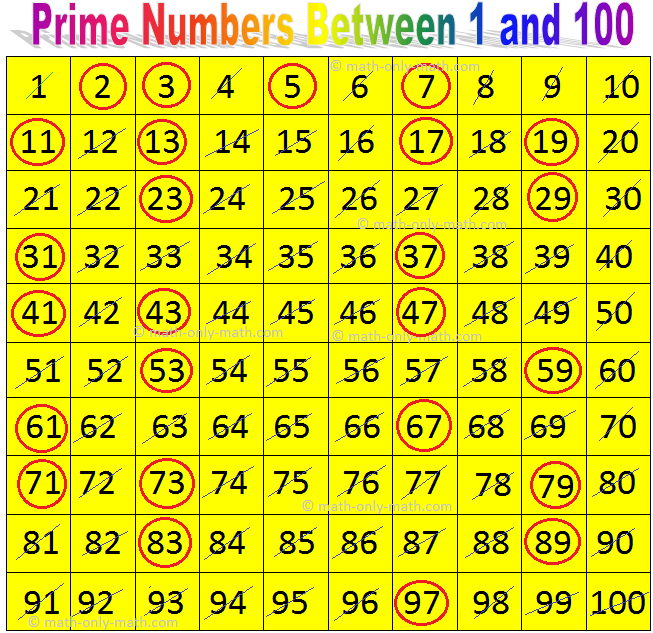
Prime Numbers Between 1 and 100

The Sieve of Eratosthenes: This is a simple method to find out the prime numbers. This method was invented by a Greek astronomer Eratosthenes about 230 B.C.

Let us find all the prime numbers between 1 and 100.

Steps:

(i) 1 is not a prime number. Cross it.

(ii) 2 is a prime number. Circle 2 and cross out all the multiples of 2.

(iii) The next prime number is 3. Circle 3 and cross out all the multiples of 3.

(iv) The next prime number is 5. Circle 5 and cross out all the multiples of 5.

(v) The next prime number is 7. Circle 7 and cross out all the multiples of 73.

(vi) The next prime number is 11. Circle 11 and cross out all the multiples of 11.

(vii) The next prime number is 13. Circle 13 and cross out all the multiples of 13.

(viii) The next prime number is 17. Circle 17 and cross out all the multiples of 17.

(ix) The next prime number is 19. Circle 19 and cross out all the multiples of 19.

(x) The next prime number is 23. Circle 23 and cross out all the multiples of 23.

(xi) Continue the process till all the numbers are either circled or cross out.

REMEMBER:

All prime numbers except 2 are odd numbers. But it is not necessary. But it is not necessary that every odd number is a prime number.

For example: 25 is an odd number, but it is not a prime number.

The least prime number is 2.

Solved Examples on Composite Numbers:

1. Which of the following is a composite number?

(a) 81

(b) 37

(c) 17

(d) 19

Solution:

We get;

81 = 1 × 81 = 3 × 27 = 9 × 9

37 = 1 × 37

17 = 1 × 17

19 = 1 × 19

Since 81 has more than two factors i.e., 1, 3, 9, 27, 81.

Therefore, 81 is a composite number, where as 37, 17 and 19 are prime numbers.

So, the option (a) is correct. 

2. List all the composite numbers between the following:

(i) 10 and 18

(ii) 61 and 69

(iii) 91 and 96

Solution:

(i) Composite numbers between 10 and 18 are 12, 14, 15 and 16.

(ii) Composite numbers between 61 and 69 are 62, 63, 64, 65, 66 and 68.

(iii) Composite numbers between 91 and 96 are 92, 93, 94 and 95.

Solved Example on Prime and Composite Numbers:

Identify prime numbers and composite numbers in the given numbers 3, 8, 17, 23, 25, 32, 41, 44.

3 = 3 × 1, factor of 3 are 3 and 1.

8 = 1 × 8, 8 = 2 × 4, factor of 8 are 1, 2, 4 and 8.

17 = 1 × 17, factor of 17 are 1 and 17.

23 = 1 × 23, factor of 23 are 1 and 23.

25 = 1 × 25, 25 = 5 × 5, factor of 25 are 1, 5 and 25.

32 = 1 × 32, 32 = 2 × 16, 32 = 4 × 8, factor of 32 are 1, 2, 4, 8, 16 and 32.

41 = 1 × 41, factor of 41 are 1 and 41.

44 = 1 × 44, 44 = 2 × 22, 44 = 4 × 11, factor of 44 are 1, 2, 4, 11, 22 and 44.

The numbers having only two factors are 3, 17, 23 and 41. Therefore, 3, 17, 23 and 41 are prime numbers. Composite numbers are 8, 25, 32, 36 and 44.

Worksheet on Prime and Composite Numbers:

I. Choose the right answer and fill in the blank:

(i) The only even prime number is ….…..

(a) 0

(b) 2

(c) 4

(d) 6

(ii) The number which is neither prime nor even ….…..

(a) 1

(b) 2

(c) 10

(d) 100

(iii) The number which has more than 2 factors is called a ….…..

(a) Even

(b) Odd

(c) Prime

(d) Composite

(iv) ….….. is the smallest composite number.

(a) 0

(b) 2

(c) 3

(d) 4

(v) A prime number has only ….….. factors.

(a) 0

(b) 1

(c) 2

(d) 3

(vi) A pair of numbers that do not have any common factor other than 1 are ….….. numbers.

(a) Even

(b) Co-prime

(c) Twin prime

(d) Prime

(vii) The smallest odd prime number is:

(a) 1

(b) 3

(c) 5

(d) 7

(viii) Which of the following is a prime number?

(a) 9

(b) 11

(c) 21

(d) 15

(ix) Which of the following even number is prime?

(a) 2

(b) 4

(c) 16

(d) 26

(x) Which of the following is a composite number?

(a) 19

(b) 21

(c) 23

(d) 29

(xi) Number formed by multiplying the first three prime numbers is:

(a) 50

(b) 40

(c) 30

(d) 20

Answers:

I. (i) (b) 2

(ii) (a) 1

(iii) (d) Composite

(iv) (b) 2

(v) (c) 2

(vi) (b) Co-prime

(vii) (b) 3

(viii) (b) 11

(ix) (a) 2

(x) (b) 21

(xi) (c) 30

II. Write true or false:

(i) 1 is a prime number.

(ii) There are 8 prime numbers between 1 – 20.

(iii) 12 is a prime number.

(iv) 21 has 4 factors – 1, 3, 7 and 21.

(v) 4, 6, 7, 8 and 9 are composite numbers.

(vi) Consecutive numbers are always co-prime.

Answers:

(i) false

(ii) true

(iii) false

(iv) true

(v) false

(vi) true

III. Choose all prime numbers:

12           19            7             8             9           11           15          

13           24           27           23           34           37           36

Answers:

19, 7, 11, 13, 23, 37

IV. Write all the composite numbers less than 30.

Answers:

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21,22, 24, 25, 26, 27, 28

V. Write all the prime numbers less than 20.

Answer:

2, 3, 5, 7, 11, 13, 17, 19

VI. Check if the given pair of numbers are co-primes:

(i) 15 and 38

(ii) 25 and 26

(iii) 12 and 18

Answers:

(i) co-primes

(ii) co-primes

(iii) not co-primes

VII. Fill in the blanks:

(i) The numbers with just 2 factors are called ……………………… numbers.

(ii) Smallest even prime number is ……………………….

(iii) Numbers with more than 2 factors are called ……………………… numbers.

(iv) 1 is neither ……………………… nor ……………………….

(v) All composite numbers have more than ……………………… factors.

Answers:

(i) prime

(ii) 2

(iii) composite

(iv) prime, composite

(v) 2

VIII. Circle all the composite numbers in the given box:

Answers:

15, 9, 21, 49, 35, 3393, 51

IX. Write all the prime numbers between:

(i) 1 and 20

(ii) 20 and 40

(iii) 40 and 60

(iv) 60 and 80

(v) 80 and 100

Answer:

IX. (i) 2, 3, 5, 7, 11, 13, 17 and 19.

(ii) 23, 29, 31, 37.

(iii) 41, 43, 47, 53, and 59.

(iv) 61, 67, 71, 73, and 79.

(v) 83, 89 and 97.

X. Write all the composite numbers between 1 and 40.

Answer:

X. 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40.

XI. Fill in the blanks:

(i) The smallest prime number is ................

(ii) The largest two-digits prime is  ................

(iii) Every prime number except  ................ is odd

(iv) ................ is neither a prime nor a composite number.

(vi) Since 4 has 3 factors, 4 is a  ................ number.

Answer:

XI. (i) 2

(ii) 97

(iii) 2

(iv) 1

(vi) composite

XII. State whether the following statements are true or false.

(i) There is only one natural number that is neither a prime nor a composite.

(ii) The odd number are prime numbers.

(iii) All even numbers are composite numbers.

(iv) The sum of two prime numbers is always an even number.

(v) 33 is a prime number.

Answer:

XII. (i) True

(ii) False

(iii) False

(iv) False

(v) False

XIII. Write down all the prime numbers between 10 and 20.

Answer: 11, 13, 17, 19

XIV. List all the prime numbers between 5 and 45.

Answer: 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.

XV. Write down all the prime numbers between 50 and 100.

Answer: 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

XVI. Write the smallest prime number.

Answer: The smallest prime number is 2

XVII. Is 1 a prime number?

Answer: No, 1 is not a prime number.

XVIII. What is prime number?

Answer: A natural number having only two distinct factors, (namely 1 and the number itself) is called a prime number.

XIX. What are composite numbers? 

Answer: Numbers having more than two distinct factors are known as composite numbers.

XX. Multiple Choice Questions (MCQ) on Prime and Composite Numbers:

     Tick (✔) the correct option.

(i) The numbers, which are not multiples of 2, are

(a) even;     (b) prime;     (c) composite;     (d) odd

(ii) An example of twin primes is

(a) 11, 13;     (b) 13, 15;     (c) 28, 29;      (d) 31, 33

(iii) Sum of two prime numbers is

(a) even;     (b) prime;     (c) odd;     (d) may be even or odd

(iv) A prime number has at the most

(i) 1 factor;     (ii) 2 factors;     (iii) 3 factors;     (iv) more than 3 factors

Answer:

XX. (i)  (d) odd

(ii) (a) 11, 13

(iii) (a) even

(iv)  (ii) 2 factors

XXI. Write down all the prime numbers between:

(i) 10 and 19

(ii) 16 and 27

Answer:

XXI. (i) 11, 13, 17, 19

(ii) 17, 19, 23

XXII. Check whether or not the following are composite numbers

(i) 98

(ii) 47

(iii) 35

(iv) 69

(v) 108

(vi) 19

(vii) 21

(viii) 103

Answer:

XXII. (i) The factors of 98 are 1, 2, 7, 14, 49 and 98.

So, 98 its a composite number.

(ii) The factors of 47 are 1 and 47.

So, 47 is not a composite number.

(iii) The factors of 35 are 1, 5, 7, 35.

So, 35 is a composite number.

(iv)The factors of 69 are 1, 3, 23, 69.

So, 69 is a composite number.

(v) The factors of 108 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108.

So, 108 is a composite number.

(vi) The factors of 19 are 1 and 19

So, 19 is not a composite number.

(vii) The factors of 21 are 1, 3, 7, 21.

So, 21 is a composite number.

(viii)The factors of 103 are 1 and 103

So, 103 is not a composite number.

XXIII. Check whether the given numbers are even or not:

(i) 9

(ii) 16

(iii) 25

(iv) 38

(v) 2010

(vi) 3758

(vii) 1005

Answer:

XXIII. (i) 9 = odd number

(ii) 16 = even number

(iii) 25 = odd number

(iv) 38 = even number

(v) 2010 = even number

(vi) 3758 = even number

(vii) 1005 = odd number

XXIV. Check whether the following are odd numbers or not

(i) 19

(ii) 21

(iii) 37

(iv) 100

(v) 208

(vi) 3005

(vii) 98 

Answer:

XXIV. Check whether the following are odd numbers or not

(i) 19 = odd number

(ii) 21 = odd number

(iii) 37 = odd number

(iv) 100 = even number 

(v) 208 = even number

(vi) 3005 = odd number

(vii) 98 = even number

XXV. Express each of the following numbers as the sum of twin primes:

(i) 24

(ii) 84

Answer:

XXV. (i) 24 = (11 + 13) = this is the sum of twin primes

(ii) 84 = (41 + 43) = this is the sum of twin primes

XXVI. Which of the following pairs of numbers are co-primes?

(i) 20, 25

(ii) 18, 35

Answer:

XXVI. (i) 20 = 1, 2, 4, 5, 20

              25 = 1, 5, 20

Here we can see that 5 is a common factor 

So, 20 and 25 are co-prime.

(ii) 18 = 1, 2, 3, 6, 9, 18

     35 = 1, 5, 7, 35

Here we can see that there is not a common factor 

So, 18 and 35 are no a co-prime.

XXVII. Find ten pairs of co-prime numbers.

Answer:

XXVII.  (3, 5); (4, 9); (7, 10); (20, 25); (31, 65); (8, 10); (6, 8); (15, 18); (9, 27); (15, 45)

Numbers.

● Various Types of Numbers

5th Grade Math Problems

From Prime and Composite Numbers to HOME PAGE