Subscribe to our YouTube channel for the latest videos, updates, and tips.
Multiplication of Rational Numbers
To learn multiplication of rational numbers let us recall how to multiply two fractions. The product of two given fractions is a fraction whose numerator is the product of the numerators of the given fractions and whose denominator is the product of the denominators of the given fractions.
In other words, product of two given fractions = product of their numerators/product of their denominators
Similarly, we will follow the same rule for the product of rational numbers.
Therefore, product of two rational numbers = product of their numerators/product of their denominators.
Thus, if a/b and c/d are any two rational numbers, then
a/b × c/d = a × c/b × d
Solved examples on multiplication of rational numbers:
1. Multiply 2/7 by 3/5
Solution:
2/7 × 3/5
= 2 × 3/7 × 5
= 6/35
2. Multiply 5/9 by (-3/4)
Solution:
5/9 × (-3/4)
= 5 × -3/9 × 4
= -15/36
= -5/12
3. Multiply (-7/6) by 5
Solution:
(-7/6) × 5
= (-7/6) × 5/1
= -7 × 5/6 × 1
= -35/6
4. Find each of the following products:
(i) -3/7 × 14/5
(ii) 13/6 × -18/91
(iii) -11/9 × -51/44
Solution:
(i) -3/7 × 14/5
= {(-3) × 14/(7 × 5)
= -6/5
(ii) 13/6 × -18/91
= {13 × (-18)}/(6 × 91)
= -3/7
(iii) -11/9 × 51/44
= {(-11) × (-51)}/(9 × 44)
= 17/12
5. Verify that:
(i) (-3/16 × 8/15) = (8/15 × (-3)/16)
(ii) 5/6 × {(-4)/5 + (-7)/10} = {5/6 × (-4)/5} + {5/6 × (-7)/10}
Solution:
(i) LHS = ((-3)/16 × 8/15) = {(-3) × 8}/(16 × 15) = -24/240 = -1/10
RHS = (8/15 × (-3)/16) = {8 × (-3)}/(15 × 16) = -24/240 = -1/10
Therefore, LHS = RHS.
Hence, ((-3)/16 × 8/15) = (8/15 × (-3)/16)
(ii) LHS = 5/6 × {-4/7 + (-7)/10} = 5/6 × [{(-8) + (-7)}/10}
= 5/6 × (-15)/10
= 5/6 × (-3)/2 = {5 × (-3)}/(6 × 2) = -15/12 = -5/4
RHS = {5/6 × -4/5} + {5/6 ×(-7)/10}
= {5 × (-4)/(6 × 5) + { 5 × (-7)}/(6 × 10) = -20/30 + (-35)/60
= (-2)/3 + (-7)/12
= {(-8) + (-7) }/ 12 = (-15)/12 = (-5)/4
Therefore, LHS = RHS
Hence, 5/6 × (-4/5 + (-7)/10) = {5/6 × (-4)/5} + (5/6 × (-7)/10)
● Rational Numbers
Introduction of Rational Numbers
Is Every Rational Number a Natural Number?
Is Every Rational Number an Integer?
Is Every Rational Number a Fraction?
Equivalent form of Rational Numbers
Rational Number in Different Forms
Properties of Rational Numbers
Lowest form of a Rational Number
Standard form of a Rational Number
Equality of Rational Numbers using Standard Form
Equality of Rational Numbers with Common Denominator
Equality of Rational Numbers using Cross Multiplication
Comparison of Rational Numbers
Rational Numbers in Ascending Order
Rational Numbers in Descending Order
Representation of Rational Numbers on the Number Line
Rational Numbers on the Number Line
Addition of Rational Number with Same Denominator
Addition of Rational Number with Different Denominator
Properties of Addition of Rational Numbers
Subtraction of Rational Number with Same Denominator
Subtraction of Rational Number with Different Denominator
Subtraction of Rational Numbers
Properties of Subtraction of Rational Numbers
Rational Expressions Involving Addition and Subtraction
Simplify Rational Expressions Involving the Sum or Difference
Multiplication of Rational Numbers
Properties of Multiplication of Rational Numbers
Rational Expressions Involving Addition, Subtraction and Multiplication
Reciprocal of a Rational Number
Rational Expressions Involving Division
Properties of Division of Rational Numbers
Rational Numbers between Two Rational Numbers
8th Grade Math Practice
From Multiplication of Rational Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Average | Word Problem on Average | Questions on Average
May 19, 25 02:53 PM
In worksheet on average we will solve different types of questions on the concept of average, calculating the average of the given quantities and application of average in different problems. -
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
● Rational Numbers - Worksheets
Worksheet on Equivalent Rational Numbers
Worksheet on Lowest form of a Rational Number
Worksheet on Standard form of a Rational Number
Worksheet on Equality of Rational Numbers
Worksheet on Comparison of Rational Numbers
Worksheet on Representation of Rational Number on a Number Line
Worksheet on Adding Rational Numbers
Worksheet on Properties of Addition of Rational Numbers
Worksheet on Subtracting Rational Numbers
Worksheet on Addition and
Subtraction of Rational Number
Worksheet on Rational Expressions Involving Sum and Difference
Worksheet on Multiplication of Rational Number
Worksheet on Properties of Multiplication of Rational Numbers
Worksheet on Division of Rational Numbers
Worksheet on Properties of Division of Rational Numbers
Worksheet on Finding Rational Numbers between Two Rational Numbers
Worksheet on Word Problems on Rational Numbers
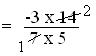
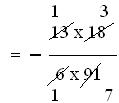
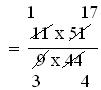
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.