Method of L.C.M.
We will discuss here about the method of l.c.m. (least common multiple).
1. Let us consider the numbers 8, 12 and 16.
Multiples of 8 are → 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, ......
Multiples of 12 are → 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, ......
Multiples of 16 are → 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, ......
The common multiple of 8, 12, 16 are 78, 96, ......
The least common multiple of 8, 12 and 16 is 48. (Smallest common multiple)
In short, the lowest common factor is expressed as L.C.M.
2. Find the L.C.M. of 3 and 4.
Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, ............
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, ............
Common multiples of 3 and 4 = 12, 24, ............
Least common multiple of 3 and 4 = 12.
3. Find the L.C.M. of 6 and 12.
Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, ............
Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, ............
Common multiples of 6 and 12 = 12, 24, 36, 48, ............
Least common multiple of 6 and 12 = 12.
Finding L.C.M.
Least Common Multiple (L.C.M.) by Prime Factorisation Method:
To find the L.C.M. we find prime factors of the given numbers.
Remember, we consider common prime factors only.
Solved Examples:
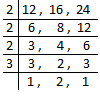
1. Find the L.C.M. of 12, 16 and 24.
First we find the prime factors of the given numbers.
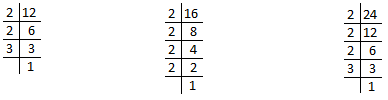
12 = 2 × 2 × 3
16 = 2 × 2 × 2 × 2
24 = 2 × 2 × 2 × 2 × 3
(2 comes maximum 4 times and 3 comes maximum once only.)
L.C.M. = 2 × 2 × 2 × 2 × 3
= 48 which is the product of their prime factors.
2. Find the L.C.M. of 10 and 16.
|
10 = 2 × 5 16 = 2 × 2 × 2 × 2 Common factor = 2 Other factors = 2, 2, 2, 5 |
2 | 10 5 |
2 | 16 2 | 8 2 | 4 2 |
Therefore, L.C.M. = 2 × 2 × 2 × 2 × 5 (common factor × other factors)
= 80
|
3. Find the L.C.M. of 20 and 25. 20 = 2 × 2 × 5 25 = 5 × 5 Common factor = 5 Other factors = 2, 2, 5 |
2 | 20 2 | 10 5 |
5 | 25 5 |
Therefore, L.C.M. = 5 × 2 × 2 × 5 (common factor × other factors)
= 100
4. Find the L.C.M. of 16 and 24.
|
16 = 2 × 2 × 2 × 2 24 = 2 × 2 × 2 × 3 Common factor = 2, 2, 2 Other factors = 2, 3 |
2 | 16 2 | 8 2 | 4 2 |
2 | 24 2 | 12 2 | 6 3 |
Therefore, L.C.M. = 2 × 2 × 2 × 2 × 3 (common factor × other factors)
= 48
Least Common Multiple (L.C.M.) by Division Method:
We can also find the L.C.M. of the given numbers by dividing all the numbers at the same time by a number that divides at least two of the given numbers.
We proceed as below:
Step I: Arrange the given numbers in a line, in any order.
Step II: Divide by a number which exactly divides at least two for the given numbers carry forward the numbers which are not divisible.
Step III: Repeat the process till neither of the two given numbers are divisible by the same number.
Step IV: The product of all the divisors and the numbers left undivided is the required LCM.
For Example:
1. Find the LCM of 24 and 30 by division method.
Solution:
LCM of 24 and 30
=2 × 2 × 2 × 3 × 5 = 120
2. Find the LCM 15, 36, and 42 by long division method.
Solution:
So. LCM of 18, 36 and 42 = 2 × 3 × 3 × 2 × 7 = 252
3. Find the LCM of 12, 16 and 24 by division method.
 |
1. When a number is not exactly divisible, we write the number itself below the line. 2. When we cannot divide the numbers by a common factor exactly we discontinue dividing the numbers. |
L.C.M. = 2 × 2 × 2 × 3 × 2 = 48
Note:
The product of L.C.M. and H.C.F. of two numbers is also the product of the numbers.
For example, the L.C.M. of 7 and 14 is 14 and the H.C.F. of 7 and 14 = 7.
We see that the product of 7 and 14 also the product of L.C.M. and H.C.F. of 7 and 14.
4. Find the L.C.M. of 25 and 45.
Therefore, L.C.M. = 5 × 5 × 9
= 225
5. Find the L.C.M. of 40, 68 and 72.
|
Steps: Divide 40, 68 and 72 by 2. 40 ÷ 2 = 20; 68 ÷ 2 = 34; 72 ÷ 2 = 36 Divide 20, 34 and 36 by 2. 20 ÷ 2 = 10; 34 ÷ 2 = 17; 36 ÷ 2 = 18 10, 17 and 18 do not have a common factor. But 10 and 18 have 2 as a common factor. Divide 10 and 18 by 2, leaving 17 as it is. 10 ÷ 2 = 5; 18 ÷ 2 = 9 5, 17 and 9 do not have a common factor. Stop the division. |
Therefore, L.C.M. = 2 × 2 × 2 × 5 × 17 × 9
= 6120
Worksheet on Method of LCM:
I. Find the L.C.M. of the following by prime factorisation method.
(i) 30, 36
(ii) 12, 15
(iii) 5, 7
(iv) 15, 30
(v) 42, 72
(vi) 12, 48
(vii) 60, 75
(viii) 25, 150
(ix) 64, 128
(x) 60, 108
Answer:
I. (i) 180
(ii) 60
(iii) 35
(iv) 30
(v) 504
(vi) 48
(vii) 300
(viii) 150
(ix) 128
(x) 540
II. Find the L.C.M. of the following by division method.
(i) 27, 84
(ii) 16, 32
(iii) 12, 15
(iv) 25, 30
(v) 60, 70
(vi) 30, 18, 60
(vii) 88, 64, 96
(viii) 48, 96, 144
(ix) 26, 28, 24
(x) 16, 12, 20
Answer:
II. (i) 756
(ii) 32
(iii) 60
(iv) 150
(v) 420
(vi) 180
(vii) 2112
(viii) 288
(ix) 2184
(x) 240
III. Find the L.C.M. of the following numbers by listing the multiples.
(i) 24, 36
(ii) 12, 18
(iii) 10, 20, 40
(iv) 27, 108
(v) 63, 84
Answer:
III. (i) 72
(ii) 36
(iii) 40
(iv) 108
(v) 252
IV. Find the L.C.M. of the following numbers:
(i) 6 and 10
(ii) 3 and 6
(iii) 10 and 12
(iv) 4 and 9
(v) 15 and 18
(vi) 6 and 11
(vii) 9 and 18
(viii) 7 and 14
(ix) 8 and 12
(x) 8 and 16
Answer:
IV. (i) 30
(ii) 6
(iii) 60
(iv) 36
(v) 90
(vi) 66
(vii) 18
(viii) 14
(ix) 24
(x) 16
V. Find the LCM by long division method:
(i) 18, 30
(ii) 13, 39
(iii) 12, 15
(iv) 38, 72
(v) 2, 3
(vi) 30, 45
(vii) 112, 140
(viii) 88, 99
Answer:
V. (i) 90
(ii) 39
(iii) 60
(iv) 1368
(v) 6
(vi) 90
(vii) 560
(viii) 792
VI. Find the LCM by long division.
Answer:
VI. (i) 315
(ii) 36
You might like these
Terms Used in Division | Dividend | Divisor | Quotient | Remainder
The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?
Successor and Predecessor | Successor of a Whole Number | Predecessor
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also
Worksheets on Comparison of Numbers | Find the Greatest Number
In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:
Number Worksheets | Practice Different Questions on Numbers | Answers
In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which
Comparison of Numbers | Compare Numbers Rules | Examples of Comparison
Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn
Formation of Numbers | Smallest and Greatest Number| Number Formation
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,
Formation of Numbers with the Given Digits |Making Numbers with Digits
In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.
Formation of Greatest and Smallest Numbers | Arranging the Numbers
the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the
Place Value | Place, Place Value and Face Value | Grouping the Digits
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are
Worksheet on Place Value | Place Value of a Digit in a Number | Math
Worksheet on place value for fourth grade math questions to practice the place value of a digit in a number. 1. Find the place value of 7 in the following numbers: (i) 7531 (ii) 5731 (iii) 5371
Worksheet on Expanded form of a Number | Expanded Form of a Number
Worksheet on expanded form of a number for fourth grade math questions to practice the expanded form according to the place values of its digit. 1. Write the expanded form of the following numbers
Examples on the Formation of Greatest and the Smallest Number |Example
In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.
Worksheet on Formation of Numbers | Questions on Formation of Numbers
In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students
Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number
Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up
From Method of L.C.M. to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 12, 24 11:42 PM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si… -
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver… -
Points and Line Segment | Two Points in a Curved Surface | Curve Line
Dec 09, 24 01:08 AM
We will discuss here about points and line segment. We know when two lines meet we get a point. When two points on a plane surface are joined, a straight line segment is obtained.
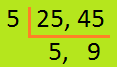
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.