Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Line-Segment, Ray and Line
Definition of in Line-segment, ray and line geometry:
Line Segment:
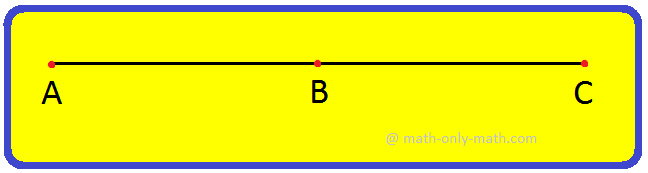
A line segment is a fixed part of a line. It has two end points. It is named by the end points. In the figure given below end points are A and B. So, the line segment is called AB. A line segment is denoted as \(\overline{AB}\).
Definition of Line Segment:
A line segment is a portion of a line with two fixed end points.
For Example: An edge of a box, a tube light, the edge of a postcard, etc. are example of line segments.
The part of a line is called a line-segment as shown below.
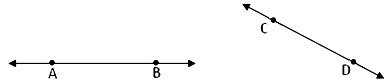
|
Line segment \(\overline{AB}\) |
Line segment \(\overline{AB}\) |
Only one line can be drawn passing through any two points but a number of lines can be drawn through a point.

|
Line AB |
|
Working Rules to Draw a Line Segment:
Step I: Let P and Q be any two points in a plane.
Step II: Let 'ℓ' be the line passing through P and Q.
Step III: The portion of the line 'ℓ' between points P and Q is called the line segment PQ or \(\overline{PQ}\).
Line segment PQ is denoted by \(\overline{PQ}\) and read as line segment PQ.
Properties of Line Segment:
1. A line segment PQ has only two end points P and Q.
2. We can draw only one line segment joining the two given points.
3. A line segment is completely known if its end points are known.
4. A line segment has length only.
Comparison of Line Segments:
In the adjoining figure, the length of a line segment PQ is the distance from one end-point P to the other end-point Q.
Working Rules to Compare Two Line Segments:
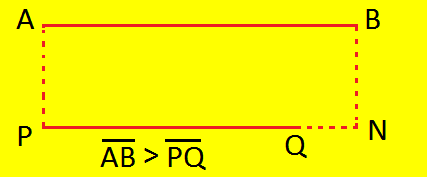
Step I: Compare a line segment AB with another line segment PQ.
Step II: Put one end of the divider at A and open the other end such that it coincides with B. Keep it open in this position.
Step III: Place one end of the divider at P. Now allow the other end to fall on the line segment PQ.
There are three possibilities:
|
(i) The other end of the divider may fall on Q. In this case, we can say that \(\overline{AB}\) and \(\overline{PQ}\) are congruent i.e., \(\overline{AB}\) ≅ \(\overline{PQ}\) or \(\overline{AB}\) = \(\overline{PQ}\). |
|
(ii) The other end of the divider may fall at a point M, between P and Q. In this case, we write \(\overline{AB}\) < \(\overline{PQ}\) i.e., (\(\overline{AB}\) is less than \(\overline{PQ}\)). |
|
(iii) The other end of the divider may fall at a point N beyond Q. In this case, we write \(\overline{AB}\) > \(\overline{PQ}\) i.e., (\(\overline{AB}\) is greater than \(\overline{PQ}\)) |
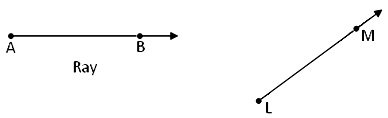
Ray:
We know about sun-rays. A sun-ray starts from the sun and goes on a direction up to endless space. Similarly a geometrical ray is considered a special kind of line which starts from a fixed point and goes to any distance to the other direction of the starting point.
Definition of Ray:
A ray is also a part of a line which has only one end point and can be extended endlessly in one direction.
A ray has no breadth or thickness.
A ray is represented by (\(\underset{AB}{\rightarrow}\)). It shows that A is the fixed point and B is a point on the path of a ray.
For Examples
Light coming from sun or torch is an example of a ray.
The name of a ray is given with two capital letters. One letter is written at the starting point of the ray and the other letter is written near the arrow end as AB and LM.
A line, line segment and ray all are called one dimensional (1-D) figures as they have only length.
In short, a ray is a portion of line. It has one end point. A ray can be extended in any one direction endlessly. We name the given ray as \(\underset{AB}{\rightarrow}\). The first letter shows the end point. The Sun light is an example of the ray.
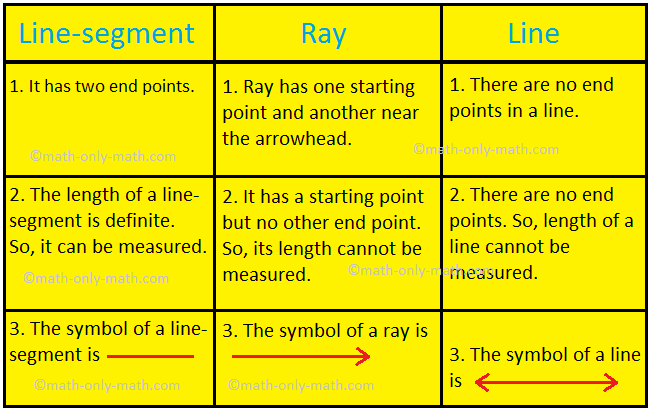
Distinction between line-segment, ray and line:
|
Line-segment 1. It has two end points. |
Ray 1. Ray has one starting point and another near the arrowhead. i.e., It has one-end-point. |
Line 1. There are no end points in a line. |
|
2. The length of a line-segment is definite. So, it can be measured. i.e., It has definite length. |
2. It has a starting point but no other end point. So, its length cannot be measured. i.e., It has no length. |
2. There are no end points. So, length of a line cannot be measured. i.e., A line has no definite length. |
|
3. It has no thickness. |
3. It has no thickness. |
3. A line has no thickness. |
|
4. The symbol of a line-segment is _____ For Example: A line AB is written as \(\overline{AB}\). |
4. The symbol of a ray is → For Example: A line AB is written as \(\overrightarrow{AB}\). |
4. The symbol of a line is ↔ For Example: A line AB is written as \(\overleftrightarrow{AB}\). |
These explanations on line-segment, ray and line will help the kids to understand the different fundamental element of geometry and their distinction.
Properties of Lines:
I. A line has no end points. A line can be named in the following two ways:
(i) Two points, say A and B, are marked on the line and the line is named as \(\overleftrightarrow{AB}\) and read as line AB.
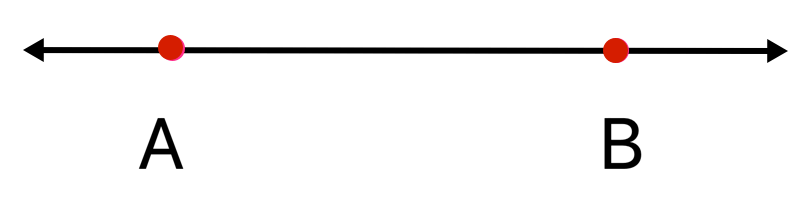
(ii) A line is also named by a small letter of alphabet, such as 'l'
B
II. We mark arrowheads on the two ends of any model of a line. These arrowheads indicate that the line extends infinitely in both the directions.
The following figure represents the model of a line 'l'.
III. We can draw an unlimited number of lines passing through a point
IV. We can mark an unlimited number of points on a given line.
Note:
How many lines can be drawn passing through the three points?
Only one single line, can be drawn only when three points are collinear.
Otherwise, there cannot be a single line drawn passing through the three points.
Related Concepts
● Geometrical Design and Models
From Line-Segment Ray and Line to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
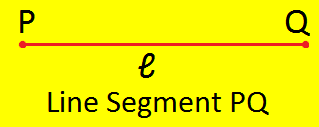








New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.