Common Solid Figures
In third grade geometry we will discuss in
brief about some of the common solid figures named below:
(i) Cube: Definition of cube, parts of a cube, properties of a cube.
(ii) Cuboid: Definition of cuboid
(iii) Cylinder: Definition of cylinder
(iv) Cone: Definition of cone
(v) Sphere: Definition of sphere
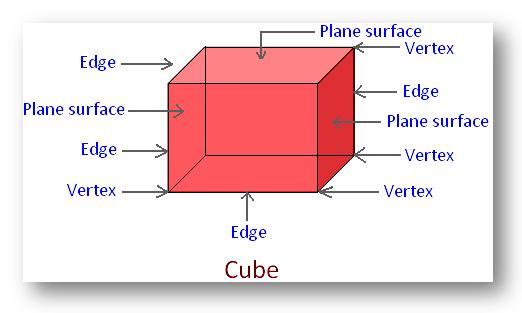
Definition of a cube:
An object which looks like solid box-shaped that has six identical square faces.
A cube has 6 equal and plane surfaces. All the faces of a cube are square in shape.
In a cube there are 6 plane surfaces. There are 8 vertices and 12 edges.
Two adjoining plane – surfaces meet at an edge. There are 12 edges in a cube and all the 12 edges are equal in length. These edges are straight edges.
The meeting point of two edges is called a vertex. In a cube there are 8 such vertices.
Parts of a cube:
(i) Face: Face is also known as sides. A cube has six faces and all the faces of a cube are square in shapes. Each face has four equal sides.
(ii) Edge: When two edges meet each other a line segment formed. There are 12 edges in a cube. All the 12 edges are equal in length because all faces are squares. These edges are straight edges.
(iii) Vertex: When three edges meet each other a point formed. There are 8 vertices in a cube.
(iv) Face Diagonals: Face Diagonals of a cube is the line segment that joins the opposite vertices of a face. There are 2 diagonals in each face so altogether there are 12 diagonals in the cube.
(v) Space Diagonals: Space diagonals of a cube are the line segment that joins the opposite vertices of a cube, cutting through its interior. There are 4 space diagonals in a cube.
Properties of a cube:
Volume: The volume of a cube is s3 where s is the length of one edge.Surface Area: The surface area of a cube is 6s2, where s is the length of one edge.
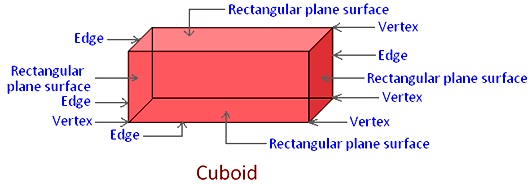
Definition of cuboid:
The cuboid has 6 rectangular faces. The opposite rectangular plane surfaces are identical (equal in all respects). It has 8 vertices and 12 edges.
In a cuboid there are 6 rectangular plane surfaces. There are 8 vertices and 12 edges.
A cube is also a cuboid having all its 6 faces equal and square. Thus, a cube has all the six faces identical, whereas a cuboid has the opposite faces identical.
Properties of a cuboid:
Formulas for the above rectangular box:
Volume: The volume of a cuboid is lwh, where l is the length, w is the width and h is the height.
Lateral Surface Area: The lateral surface area of a cuboid is 2lh + 2wh, where l is the length, w is the width and h is the height.
Surface Area: The surface area of a cuboid is 2lw + 2lh + 2wh, where l is the length, w is the width and h is the height.
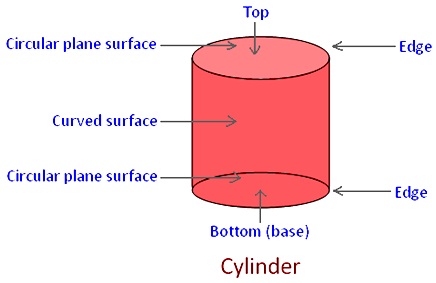
Definition of cylinder:
A cylinder stands on a circular plane surface having circular plane surfaces on its top and bottom. Thus a cylinder has two circular plane surfaces, one at its base and another at its top. It has a curved surface in the middle.
It has two edges, at which the two plane surfaces meet with the curved surface. These edges are curved edges.
In a cylinder there are 2 plane surfaces and 1 curved surface. There are 2 edges and no vertices.
The base and top of a cylinder are of the same shape (circular) and size. Thus, both are identical.
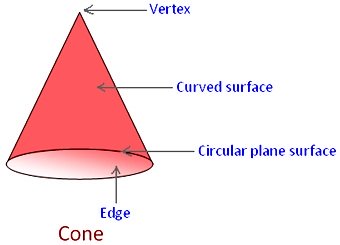
Definition of cone:
A cone has one plane circular surface, i.e. its base and only one curved surface. In a cone there is 1 plane surface and 1 curved surface. There are 1 edge and 1 vertex.
It has one edge which is formed by the circular plane surface meeting with the curved surface. The edge of a cone is a curved edge.
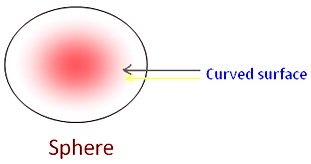
Definition of sphere:
The ball-like shape is called a sphere. In sphere there is curve surface, no edge and no vertex.
Some of the common solid figures are explained above in brief with the labeled diagram to get the basic ideas of the solid shapes.
Note:
(i) The surface of solid is called face.
(ii) Edge is formed when two faces meet.
(iii) The point where 3 faces meet is called the corner.
Related Concepts
● Geometrical Design and Models
From Common Solid Figures to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Counting Numbers from 1 to 50 | Match the Number | Missing Numbers
Apr 04, 25 03:46 PM
In counting numbers from 1 to 50, recognize the numbers, count and then join the numbers in the correct number order. Here we mainly need eye-hand coordination to draw the picture and maintain the num -
Counting Eleven to Twenty with Numbers and Words |Numbers from 11 - 20
Apr 04, 25 03:21 PM
Counting eleven to twenty with numbers and words are explained below. One ten and one more is eleven. Eleven comes after ten. One ten and two more is twelve. Twelve comes after eleven. -
5th Grade BODMAS Rule Worksheet | PEMDAS | Order of operations|Answers
Apr 03, 25 03:11 PM
In 5th Grade BODMAS Rule Worksheet you will get different types of problems on mathematical expressions involving different operations, mathematical expression with 'brackets' and 'of' and simplifying… -
Worksheet on Simplification | Simplify Expressions | BODMAS Questions
Apr 03, 25 02:58 PM
In worksheet on simplification, the questions are based in order to simplify expressions involving more than one bracket by using the steps of removal of brackets. This exercise sheet -
Divisible by 2 Video |Test of Divisibility by 2 Trick| Rules| Examples
Apr 03, 25 10:25 AM
A number is divisible by 2 if the digit at unit place is either 0 or multiple of 2. So a number is divisible by 2 if digit at its units place is 0, 2, 4, 6 or 8.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.