Subscribe to our βΆοΈ YouTube channel π΄ for the latest videos, updates, and tips.
Intersection of Sets using Venn Diagram
Learn how to represent the intersection of sets using Venn diagram. The intersection set operations can be visualized from the diagrammatic representation of sets.
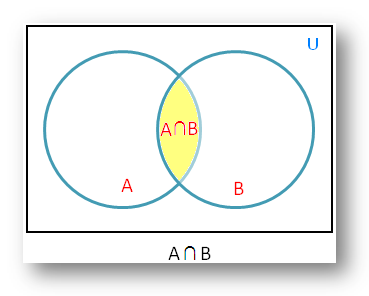
The rectangular region represents the universal set U and the circular regions the subsets A and B. The shaded portion represents the set name below the diagram.
Let A and B be the two sets. The intersection of A and B is the set of all those elements which belong to both A and B.
Now we will use the notation A β© B (which is read as βA intersection Bβ) to denote the intersection of set A and set B.
Thus, A β© B = {x : x β A and x β B}.
Clearly, x β A β© B
β x β A and x β B
Therefore, the shaded portion in the adjoining figure represents A β© B.
Thus, we conclude from the definition of intersection of sets that A β© B β A, A β© B β B.
From the above Venn diagram the following theorems are obvious:
(i) A β© A = A (Idempotent theorem)
(ii) A β© U = A (Theorem of union)
(iii) If A β B, then A β© B = A.
(iv) A β© B = B β© A (Commutative theorem)
(v) A β© Ο = Ο (Theorem of Ο)
(vi) A β© Aβ = Ο (Theorem of Ο)
The symbols β and β© are often read as βcupβ and βcapβ respectively.
For two disjoint sets A and B, A β© B = Ο.
Solved examples of
intersection of sets using Venn diagram:
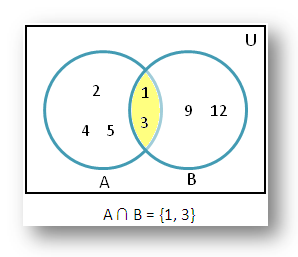
1. If A = {1, 2, 3, 4, 5} and B = {1, 3, 9, 12}. Find A β© B using venn diagram.
Solution:
According to the given question we know, A = {1, 2, 3, 4, 5} and B = {1, 3, 9, 12}
Now letβs draw the venn diagram to find A intersection B.
Therefore, from the venn diagram we get A β© B = {1, 3}
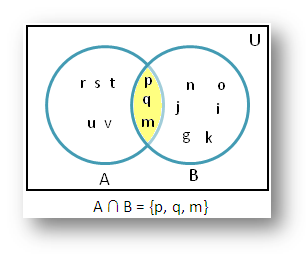
2. From the adjoining figure find A intersection B.
Solution:
According to the adjoining figure we get;
Set A = {m, p, q, r, s, t, u, v}
Set B = {m, n, o, p, q, i, j, k, g}
Therefore, A intersection B is the set of elements which belong to both set A and set B.
Thus, A β© B = {p, q, m}
β Set Theory
β Sets Theory
β Types of Sets
β Finite Sets and Infinite Sets
β Power Set
β Problems on Intersection of Sets
β Problems on Complement of a Set
β Problems on Operation on Sets
β Venn Diagrams in Different Situations
β Relationship in Sets using Venn Diagram
β Union of Sets using Venn Diagram
β Intersection of Sets using Venn Diagram
β Disjoint of Sets using Venn Diagram
β Difference of Sets using Venn Diagram
8th Grade Math Practice
From Intersection of Sets using Venn Diagram to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.