Four Digit Numbers

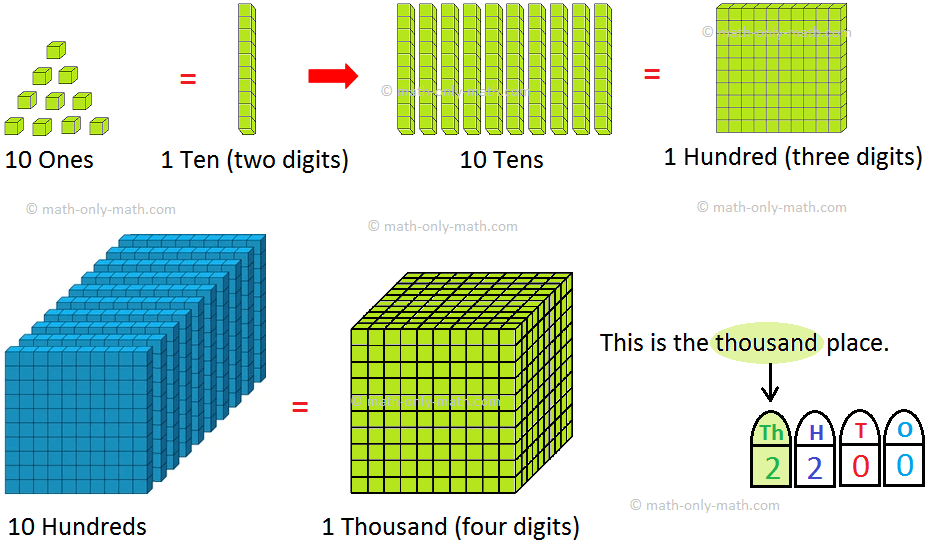
We have learned one, two and three digits numbers.

Now, we will study four digit numbers.

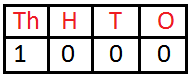
We add 1 to 999 to get the smallest four digit number. eg. 999 + 1 = 1000.

4-Digit Numbers


What are Four Digit Numbers?

We may divide 4-digit numbers in 9 groups.

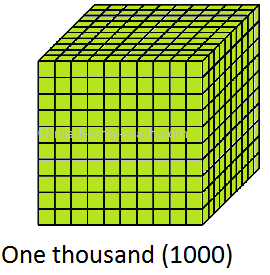
(i) 1000 to 1999 (one thousand to one thousand nine hundred ninety nine)

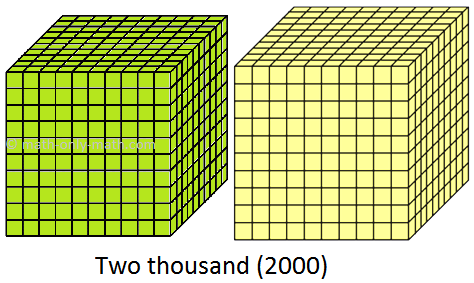
(ii) 2000 to 2999 (two thousand to two thousand nine hundred ninety nine)

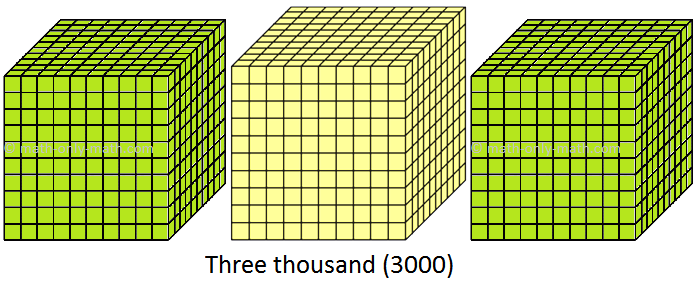
(iii) 3000 to 3999 (three thousand to three thousand nine hundred ninety nine)

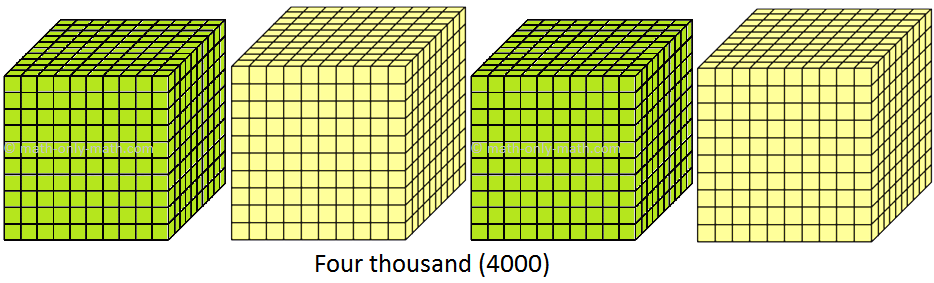
(iv) 4000 to 4999 (four thousand to four thousand nine hundred ninety nine)

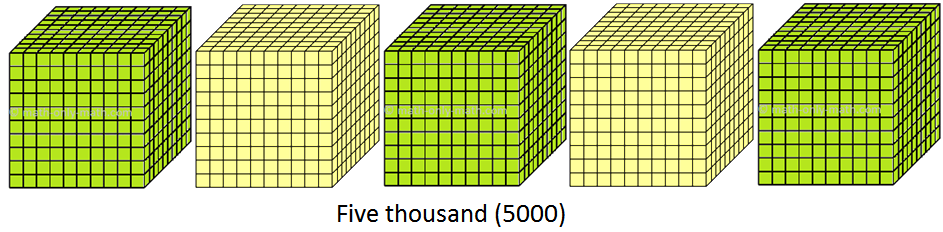
(v) 5000 to 5999 (five thousand to five thousand nine hundred ninety nine)

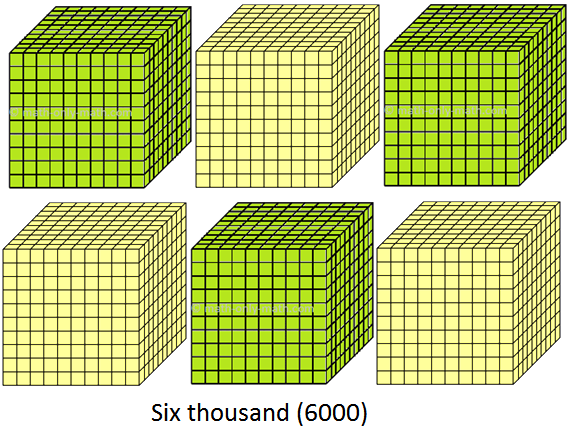
(vi) 6000 to 6999 (six thousand to six thousand nine hundred ninety nine)

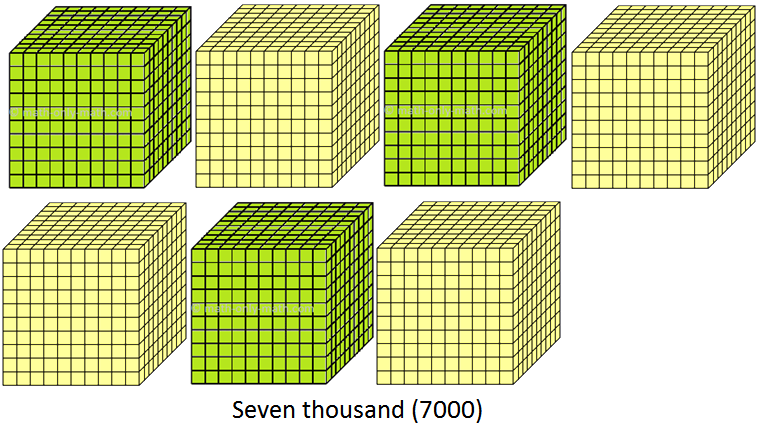
(vii) 7000 to 7999 (seven thousand to seven thousand nine hundred ninety nine)

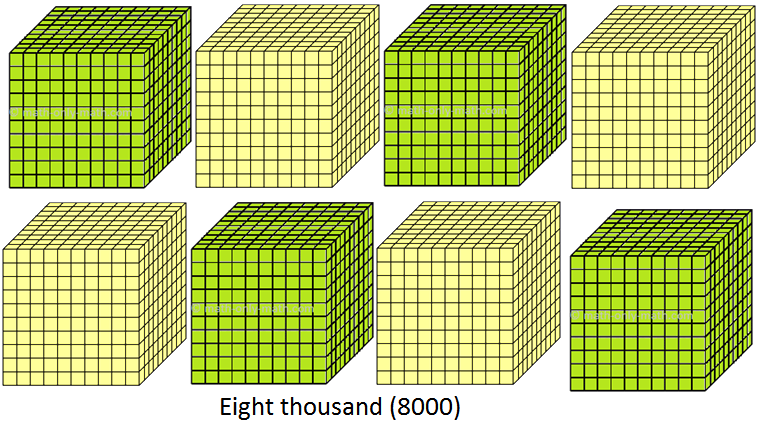
(viii) 8000 to 8999 (eight thousand to eight thousand nine hundred ninety nine)

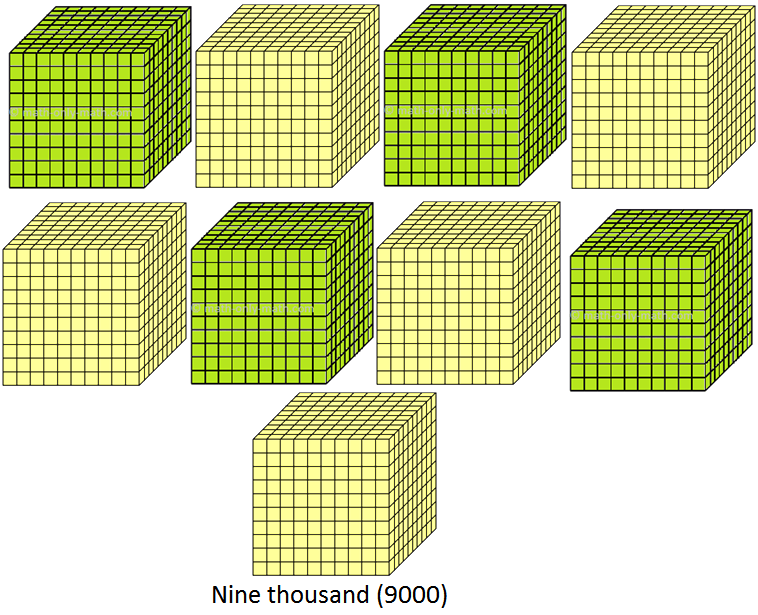
(ix) 9000 to 9999 (nine thousand to nine thousand nine hundred ninety nine)

Note: Four digit numbers begin with 1000.


Four Digits Numbers in Thousands:

One Thousand
Two Thousand
Three Thousand
Four Thousand
Five Thousand
Six Thousand
Seven Thousand
Eight Thousand
Nine Thousand


If all the numbers of one digit, then two digits and then three digits are placed step by step to the right of 1 Thousand according to their place values, the numbers from 1001 to 1999 are formed.

1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010, 1011, 1012, 1013, 1014, 1015, 1016, 1017, 1018, 1019, 1020, 1021, 1022, 1023, 1024, 1025, 1026, 1027, 1028, 1029, 1030, 1031, 1032, 1033, 1034, 1035, 1036, 1037, 1038, 1039, 1040, 1041, 1042, 1043, 10144, 1045, 1046, 1047, 1048, 1049, 1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057, 1058, 1059, 1060, 1061, 1062, 1063, 1064, 1065, 1066, 1067, 1068, 1069, 1070, 1071, 1072, 1073, 1074, 1075, 1076, 1077, 1078, 1079, 1080, 1081, 1082, 1083, 1084, 1085, 1086, 1087, 1088, 1089, 1090, 1091, 1092, 1093, 1094, 1095, 1096, 1097, 1098, 1099, 1110, 1111, …………………., 1199, 1200, …………………., 1299, 1300, 1301, …………………………., 1399, 1400, …………………, 1499, 1500, 1501, …………………., 1899, 1900, 1901, ………………….., 1921, …………………., 1971, …………………., 1981, ………………………, 1991, …………………., 1999. Similarly, 2000, …………….., 2199, ………………….., 2299, ……………………, 2799, ……………………, 2899, ………………….., 2999 are formed. Thus, we reach upto 3999, ……………….., 4999, …………………, 5999, …………………, 6999, …………………, 7999, …………………, 8999, ………………….., 9999.



Shown below are some four digit numbers on the abacus:

Four Digit Numbers

2354

Two thousand three hundred fifty four

Four Digit Number

5241

Five thousand two hundred forty one


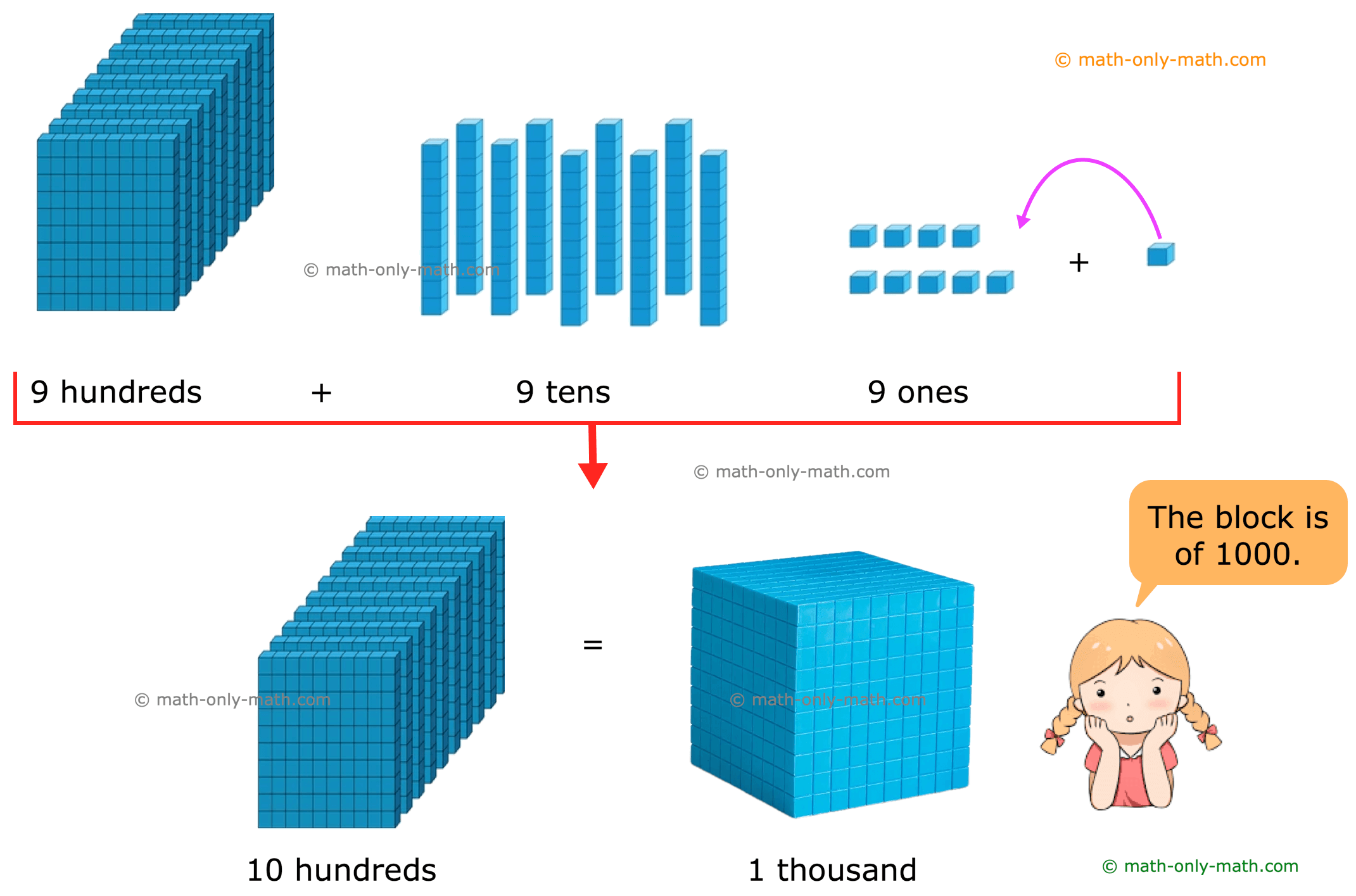
Mike has 999 lollipops. He has made 9 packets of 100 lollipops in each. He is now left with 99 lollipops. How many more lollipops does Mike need to make another packet of 100 lollipops?

99 + 1 = 100

4-Digit Numbers

By having 1 more lollipop, Mike can make another packet of 100 lollipops.

Mike has now 10 packets of 100 lollipops in each.

4-Digit Numbers '1000'

10 hundreds = 1 thousand = 1000

Thus, Mike has 1000 lollipops in all. 1000 is a 4-digit number and is read as ‘one thousand’.

1 packet = 100 lollipops

2 packets = 100 + 100 = 200 lollipops

3 packets = 200 + 100 = 300 lollipops

4 packets = 300 + 100 = 400 lollipops

5 packets = 400 + 100 = 500 lollipops

6 packets = 500 + 100 = 600 lollipops

7 packets = 600 + 100 = 700 lollipops

8 packets = 700 + 100 = 800 lollipops

9 packets = 800 + 100 = 900 lollipops

1000

1000 is the smallest 4-digit number. 9999 is the largest 4-digit number.

Digit

One-digit

Two-digit

Three-digit

Four-digit

Largest Number

9

99

999

9999

Smallest Number

0

10

100

1000


9 + 1 = 10

99 + 1 = 100

999 + 1 = 1000

Numbers Beyond 999:

We know that, 

The greatest 3-digit number is 999.

If we add 1 to 999, we get 1000. 

1000 is the smallest 4-digit number, we read it as one hundred.

Formation of 1000


Counting by Thousands: 

The red digit tells us how many thousands.

1000  -  _______

2000  -  _______

3000  -  _______

4000  -  _______

5000  -  _______

6000  -  _______

7000  -  _______

8000  -  _______

9000  -  _______


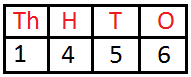
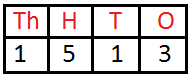
Let us now learn some 4-digit number names.

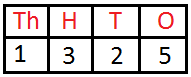
4-Digit Numbers 1325
1325

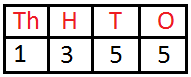
1325 is read as ‘One thousand three hundred twenty-five’

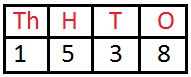
4-Digit Numbers 1538
1538

1538 is read as ‘One thousand five hundred thirty-eight’

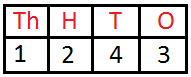
4-Digit Numbers 1243
1243

1243 is read as ‘One thousand two hundred forty-three’

4-Digit Numbers 1456
1456

1456 is read as ‘One thousand four hundred fifty-six’

4-Digit Numbers 1513
1513

1513 is read as ‘One thousand five hundred thirteen’

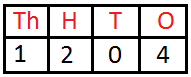
4-Digit Numbers 1204
1204

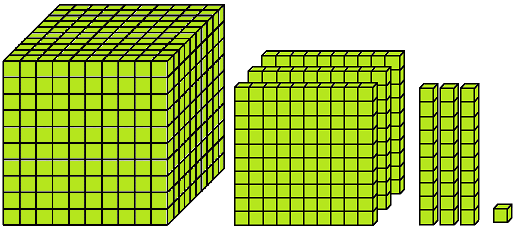
1204 is read as ‘One thousand two hundred four’

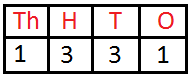
4-Digit Numbers 1331
1331

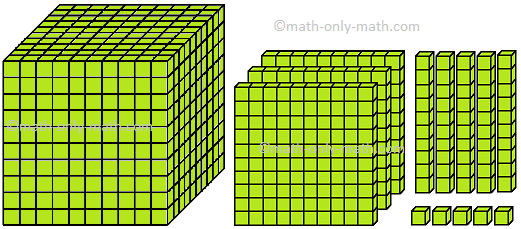
1331 is read as ‘One thousand three hundred thirty-one’

4-Digit Numbers 1355
1355

1355 is read as ‘One thousand three hundred fifty-five’

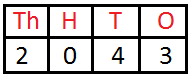
4-Digit Numbers 2043
2043

2043 is read as ‘Two thousand forty-three’

Note: 1. The largest 4-digit number is 9999.

          2. The smallest 4-digit number is 1000.


Forming Four Digit Numbers:

Forming 4-Digit Numbers


4-Digit Numbers in Expand Form and Short Form:

(i) 1 thousand + 4 hundreds + 6 tens + 4 ones

(ii) 2 thousand + 6 hundreds + 3 tens + 1 one

(iii) 5 thousand + 1 hundred + 3 tens + 2 ones

(iv) 9 thousand + 9 hundreds + 9 tens + 9 ones

(v) 4 thousands + 5 hundreds + 0 tens + 3 ones

(vi) 6 thousands + 3 hundreds + 0 tens + 0 ones

(vii) 7 thousands + 2 hundreds + 2 tens + 5 ones

(viii) 3 thousands + 0 hundred + 1 ten + 6 ones

(ix) 8 thousands + 7 hundreds + 4 tens + 7 ones

(x) 1 thousand + 8 hundreds + 5 tens + 8 ones

(xi) 2 thousands + 5 hundreds + 7 tens + 9 ones

(xii) 1 thousand + 4 hundreds + 6 tens + 9 ones

= 1000 + 400 + 60 + 4

= 2000 + 600 + 30 + 1

= 5000 + 100 + 30 + 2

= 9000 + 900 + 90 + 9

= 4000 + 500 + 0 + 3

= 6000 + 300 + 0 + 0

= 7000 + 200 + 20 + 5

= 3000 + 0 + 10 + 6

= 8000 + 700 + 40 + 7

= 1000 + 800 + 50 + 8

= 2000 + 500 + 70 + 9

= 1000 + 400 + 60 + 9

 = 1460

 = 2631

 = 5132

 = 9999

 = 4503

 = 6300

 = 7225

 = 3016

 = 8747

 = 1858

 = 2579

 = 1469

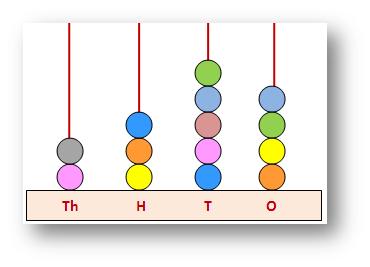
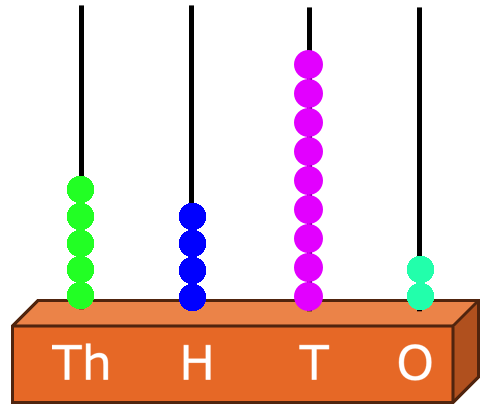
Four Digit Numbers on Abacus:

We can also form numbers using a spike abacus.

This abacus has four rods, one each for thousands, hundreds, tens and the ones place.

Blank Abacus 4-Digit Number

For Example:

Which number is formed by the beads on this abacus?

Blank Abacus Shows the Numbers

Solution:


This abacus shows the number
This Abacus Shows the Number 5492


Forms of Four Digit Numbers:

I. Write in the short forms. One has been done for you.

(i) 2000 + 700 + 50 + 8  

(ii) 3000 + 400 + 60 + 2

(iii) 1000 + 300 + 40 + 5

(iv) 4000 + 200 + 30 + 5

(v) 6000 + 200 + 70 + 9

(vi) 5000 + 800 + 60 + 7

(vii) 7000 + 100 + 60 + 5

(viii) 8000 + 900 + 80 + 4

(ix) 9000 + 500 + 30 + 6

(x) 3000 + 800 + 00 + 2

 = 2758

 = ___________

 = ___________

 = ___________

 = ___________

 = ___________

 = ___________

 = ___________

 = ___________

 = ___________

Answer:

1. (ii) 3462

(iii) 1345

(iv) 4235

(v) 6279

(vi) 5867

(vii) 7165

(viii) 8984

(ix) 9536

(x) 3802


II. Write in the long forms. One has been done for you.

(i) 7684

(ii) 5053

(iii) 6734

(iv) 8635

(v) 9896

(vi) 3338

(vii) 4725

(viii) 2431

(ix) 1876

(x) 3707

(xi) 2980

(xii) 8579

 = 7000 + 600 + 80 + 4

 = __________________

 = __________________

 = __________________

 = __________________

 = __________________

 = __________________

 = __________________

 = __________________

 = __________________

 = __________________

 = __________________

Answer:

2. (ii) 5000 + 0 + 50 + 3

(iii) 6000 + 700 + 30 + 4

(iv) 8000 + 600 + 30 + 5

(v) 9000 + 800 + 90 + 6

(vi) 3000 + 300 + 30 + 8

(vii) 4000 + 700 + 20 + 5

(viii) 2000 + 400 + 30 + 1

(ix) 1000 + 800 + 70 + 6

(x) 3000 + 700 + 0 + 7

(xi) 2000 + 900 + 80 + 0

(xii) 8000 + 500 + 70 + 9


Writing Four Digit Numbers:

III. Write in numbers:

(i) Five thousand eight hundred and fifty three

(ii) Nine thousand and two hundred

(iii) Two thousand eight hundred and four

(iv) Six thousand five hundred and ten

(v) Three thousand seven hundred and ninety five

(vi) One thousand nine hundred and forty two

(vii) Four thousand six hundred and eighty six

(viii) Seven thousand four hundred and sixty six

(ix) Eight thousand three hundred and seventy nine

(x) Three thousand nine hundred and thirty four

(xi) Two thousand five hundred and eighty seven

(xii) Four thousand two hundred and thirty five

(xiii) Seven thousand nine hundred and eight


Answer:

III. (i) 5853

(ii) 9200

(iii) 2804

(iv) 6510

(v) 3795

(vi) 1942

(vii) 4686

(viii) 7466

(ix) 8379

(x) 3934

(xi) 2587

(xii) 4235

(xiii) 7908


IV. Write the number names:

(i) 1530

(ii) 9217

(iii) 5645

(iv) 4872

(v) 3356

(vi) 2968

(vii) 1530

(viii) 6729

(ix) 8800

(x) 2874

(xi) 3507

(xii) 4235

(xiii) 6879


Answer:

IV. (i) One thousand five hundred thirty

(ii) Nine thousand two hundred seventeen

(iii) Five thousand six hundred forty five

(iv) Four thousand eight hundred seventy two

(v) Three thousand three hundred fifty six

(vi) Two thousand nine hundred sixty eight

(vii) One thousand five hundred thirty

(viii) Six thousand seven hundred twenty nine

(ix) Eight thousand eight hundred

(x) Two thousand eight hundred seventy four

(xi) Three thousand five hundred seven

(xii) Four thousand two hundred thirty five

(xiii) Six thousand eight hundred seventy nine


Four Digit Numbers Fun:

V. Write forward consecutive numbers:

(i) 1001, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(ii) 1340, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(iii) 2550, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(iv) 3025, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(v) 4386, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(vi) 5991, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(vii) 6033, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(viii) 7732, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..


Answer:

V. (i) 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010

(ii) 1341, 1342, 1343, 1344, 1345, 1346, 1347, 1348, 1349

(iii) 2551, 2552, 2553, 2554, 2555, 2556, 2557, 2558, 2559

(iv) 3026, 3027, 3028, 3029, 3030, 3031, 3032, 3033, 3034

(v) 4387, 4388, 4389, 4390, 4391, 4392, 4393, 4394, 4395

(vi) 5992, 5993, 5994, 5995, 5996, 5997, 5998, 5999, 6000

(vii) 6034, 6035, 6036, 6037, 6038, 6039, 6040, 6041, 6042

(viii) 7733, 7734, 7735, 7736, 7737, 7738, 7739, 7740, 7741


VI. Write backwards consecutive numbers

(i) 1068, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(ii) 6880, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(iii) 9999, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(iv) 5119, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(v) 3425, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..

(vi) 2500, ………….., ………….., ………….., ………….., ………….., ………….., ………….., ………….., …………..


Answer:

VI. (i) 1067, 1066, 1065, 1064, 1063, 1062, 1061, 1060, 1059

(ii) 6879, 6878, 6877, 6876, 6875, 6874, 6873, 6872, 6871

(iii) 9998, 9997, 9996, 9995, 9994, 9993, 9992, 9991, 9990

(iv) 5118, 5117, 5116, 5115, 5114, 5113, 5112, 5111, 5110

(v) 3424, 3423, 3422, 3421, 3420, 3419, 3418, 3417, 3416

(vi) 2499, 2498, 2497, 2496, 2495, 2494, 2493, 2492, 2491



VII. Complete the patterns:

(i) 8002, 8004, 8006, ………….., ………….., ………….., ………….., ………….., ………….., …………..

(ii) 9015, 9020, 9025, ………….., ………….., ………….., ………….., ………….., ………….., …………..

(iii) 7005, 7010, 7015, ………….., ………….., ………….., ………….., ………….., ………….., …………..

(iv) 6340, 6350, 6360, ………….., ………….., ………….., ………….., ………….., ………….., …………..

(v) 5000, 5006, 5012, ………….., ………….., ………….., ………….., ………….., ………….., …………..

(vi) 1100, 1200, 1300, ………….., ………….., ………….., ………….., ………….., ………….., …………..


Answer:

VII. (i) 8004, 8006, 8008, 8010, 8012, 8014, 8016, 8018, 8020

(ii) 9020, 9025, 9030, 9035, 9040, 9045, 9050, 9055, 9060

(iii) 7010, 7015, 7020, 7025, 7030, 7035, 7040, 7045, 7050

(iv) 6350, 6360, 6370, 6380, 6390, 6400, 6410, 6420, 6430

(v) 5006, 5012, 5018, 5024, 5030, 5036, 5042, 5048, 5054

(vi) 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000


VIII. Write the successor numbers (the number after) of the following four digit numbers:

(i) 4530 …………..

(ii) 6625 …………..

(iii) 2836 …………..

(iv) 1014 …………..

(v) 8590 …………..

(vi) 5417 …………..

(vii) 6879 …………..

(viii) 5792 …………..

(ix) 7876 …………..

(x) 5327 …………..

(xi) 9891 …………..

(xii) 5109 …………..

(xiii) 1999 …………..

(xiv) 3579 …………..

(xv) 4284 …………..

(xvi) 2029 …………..


Answer:

VIII. (i) 4531

(ii) 6626

(iii) 2837

(iv) 1015

(v) 8591

(vi) 5418

(vii) 6880

(viii) 5793

(ix) 7877

(x) 5328

(xi) 9892

(xii) 5110

(xiii) 1100

(xiv) 3580

(xv) 4285

(xvi) 2030


IX. Write the predecessors numbers (the number before) of the following four digit numbers:

(i) ………….. 3560

(ii) ………….. 5871

(iii) ………….. 9090

(iv) ………….. 8099

(v) ………….. 7418

(vi) ………….. 3464

(vii) ………….. 8254

(viii) ………….. 2726

(ix) ………….. 5381

(x) ………….. 7002

(xi) ………….. 3004

(xii) ………….. 3507

(xiii) …………..  6231

(xiv) ………….. 4117

(xv) ………….. 1990

(xvi) ………….. 2001


Answer:

IX. (i) 3559

(ii) 5870

(iii) 9089

(iv) 8098

(v) 7417

(vi) 3463

(vii) 8253

(viii) 2725

(ix) 5380

(x) 7001

(xi) 3003

(xii) 3506

(xiii) 6230

(xiv) 4116

(xv) 1989

(xvi) 2000


X. Write the numbers before and after:

(i) ………….. 1995 …………..

(ii) ………….. 2010 …………..

(iii) ………….. 7328 …………..

(iv) ………….. 5609 …………..

(v) ………….. 8003 …………..

(vi) ………….. 9320 …………..

(vii) …………..  6037 …………..

(viii) ………….. 5469 …………..

(ix) ………….. 7452 …………..

(x) ………….. 4230 …………..

(xi) ………….. 3000 …………..

(xii) ………….. 7989 …………..


Answer:

X. (i) 1994; 1996

(ii) 2009; 2011

(iii) 7327; 7329

(iv) 5608; 5610

(v)8002; 8004

(vi) 9319; 9321

(vii) 6036; 6038

(viii) 5468; 5470

(ix) 7451; 7453 

(x) 4229; 4231 

(xi) 2999; 3001 

(xii) 7988; 7990


XI. Write the numbers between:

(i) 3057 ………….. 3059

(ii) 1574 ………….. 1576

(iii) 3898 ………….. 3900

(iv) 6407 ………….. 6409

(v) 3281 ………….. 3283

(vi) 5000 ………….. 5002

(vii) 8342 ………….. 8344

(viii) 2318 ………….. 2320

(ix) 9836 ………….. 9838

(x) 4201 ………….. 4203

(xi) 1810 ………….. 1812

(xii) 7999 ………….. 8001


Answer:

XI. 

(i) 3058

(ii) 1575

(iii) 3899

(iv) 6408

(v) 3282

(vi) 5001

(vii) 8343

(viii) 2319

(ix) 9837

(x) 4202

(xi) 1811

(xii) 8000

Place value in 4-digits numbers:

A place value depends upon the position of a digit in a given number.

A place value keeps increasing, when a number moves from right to left.

1 one, place value = 1  1 or 1

8 tens, place value = 8  10 or 80

6 hundreds, place value = 6 100 or 600

3 thousands, place value = 4   1000 or 4000

3746 = 3 thousands + 7 hundreds + 4 tens + 6 ones

          = 3000 + 700 + 40 + 6


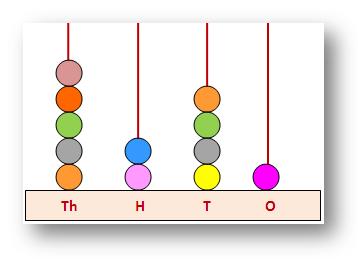
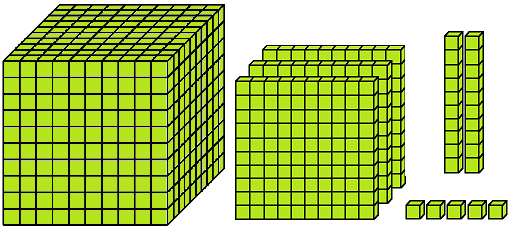
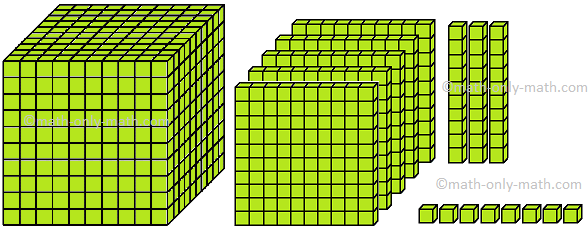
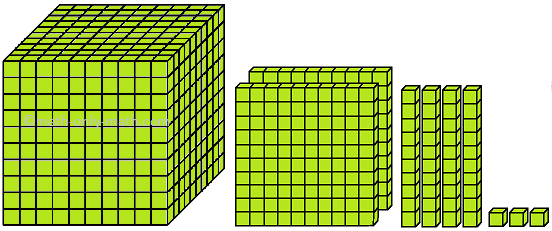
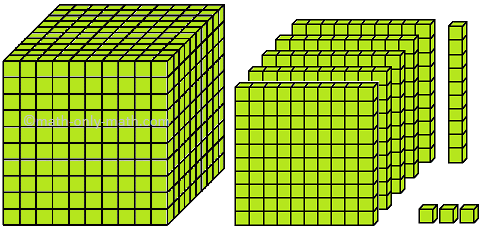
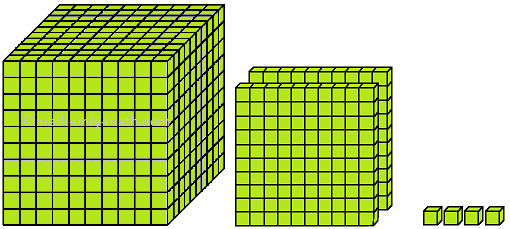
XII. Which number is formed by the following blocks?

Which Number is Formed

Solution:


This can be written as
Forming 4-Digit Number

You might like these





3rd Grade Math Lessons

From Four Digit Numbers to HOME PAGE




Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.




Share this page: What’s this?

Recent Articles

RSS

  1. 3rd Grade Math Worksheets |3rd Grade Math Sheets|3rd Grade Math Lesson

    Jan 14, 25 02:50 PM

    3rd Grade Math Worksheets
    3rd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students. Teachers and parents can also follow the worksheets to guide the students.

    Read More

  2. 3rd Grade Subtraction Worksheet | 3-Digit Subtraction Worksheets | Ans

    Jan 14, 25 01:57 PM

    Fill in the Missing Numbers Subtraction and Addition
    In 3th Grade Addition Worksheet we will solve how to subtract 3-digit numbers by expansion, subtraction of 3-digit numbers without regrouping, subtraction of 3-digit numbers with regrouping, propertie…

    Read More

  3. Facts about Subtraction | Subtraction of Small Numbers|Solved Examples

    Jan 14, 25 12:29 AM

    The operation to finding the difference between two numbers is called subtraction. Let us know some facts about subtraction which will help us to learn subtraction of large numbers. 1. Subtraction wit…

    Read More

  4. Word Problems on Subtraction |Worksheet on Subtraction Word Problems |

    Jan 14, 25 12:21 AM

    Subtraction Problem
    In word problems on subtraction we need to read the question carefully and understand what we need to find out. We know, in subtraction the larger number from which we subtract the other number (the s…

    Read More

  5. Worksheet on Estimating Sums and Differences | Find the Estimated Sum

    Jan 13, 25 01:34 PM

    Estimate the Difference
    In 4th grade worksheet on estimating sums and differences, all grade students can practice the questions on estimations.This exercise sheet on estimating sums and differences can be practiced

    Read More