Circular System
The unit of circular system is based on the constant relation that exists between the circumference of a circle and the radius of that circle.
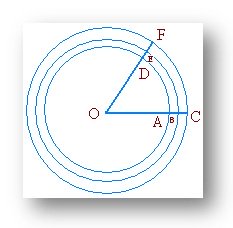
Let us take three concentric circles. From the smallest circle let us cut off an arc AD equal in length to the radius of the circle. O, A and O, D are joined. Then ∠AOD will be an angle at the centre subtended by the arc equal in length to the radius of the circle.
OA and OD are produced to meet other two circles at B, C and E, F respectively. On measurement we will find that BE and CF are equal in length to the radii of the corresponding circles.
So ∠BOE and ∠COF are angles at the centre subtended by arcs equal in length to the respective radii.
Hence we may conclude that an arc of any circle equal in length to the radius of the circle subtends at its centre an angle of constant magnitude.
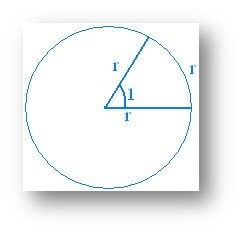
This
angle is taken as the unit of measurement of angles in the circular system.
See the magnitude of an angle of one radian in the figure.
Worked-out Examples on Circular System:
In a triangle the angles are in the ratio 2 : 5 : 3, what is the value of the least angle in radian?
Solution:
Let the angles be 2x, 5x and 3x radians.
Therefore, 2x + 5x + 3x = π
or, x = π/10
The least angle in radian is 2x = 2 · π/10 = π/5
`Basic Trigonometry
Measurement of Trigonometric Angles
Relation between Sexagesimal and Circular
Conversion from Sexagesimal to Circular System
Conversion from Circular to Sexagesimal System
From Circular System to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
|
|
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.