Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Measurement of Trigonometric Angles
In measurement of trigonometric angles the particular branch of mathematics is mainly based on the ratios of sides of a right-angled triangle with respect to the two acute angles, we should have a full discussion, about the angle what an angle is.
What is an angle?
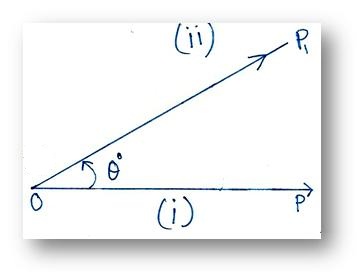
(i) An angle is formed at a point when two rays emerge from it.
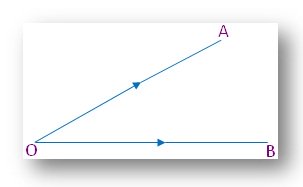
As in the above figure we can see that two rays OA and OB emerging from the point O form ∠AOB. We shall call it a geometric angle.
(ii) If the initial point of a ray (the
point from which the ray emerges) is kept fixed and the ray is rotated in a
plane in the anticlockwise direction, then the subsequent positions of the ray
make angles with the initial position at that fixed point.
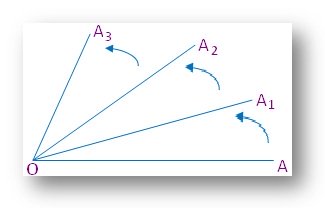 |
In this figure the initial point O of the ray OA is kept fixed and the ray OA is rotated in the anticlockwise direction to attain the positions OA1, OA2, OA3 etc. Thus ∠AOA1, ∠AOA2, ∠AOA3 etc. are formed at the point O. |
These angles are called trigonometric angles.
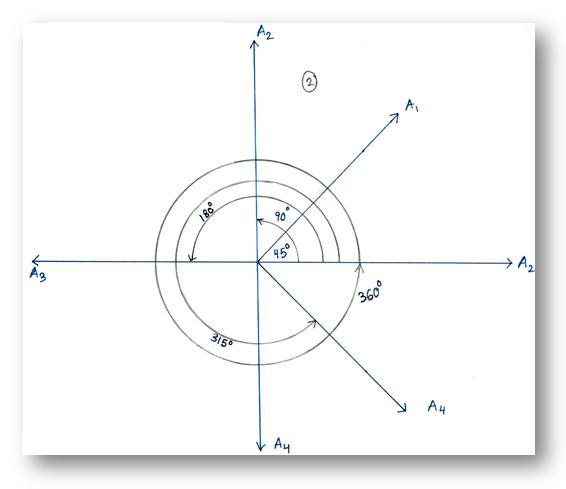
(1) It is clear from the figure that, in geometry, only the magnitude of an angle is the main thing we consider. An angle in geometry can assume any value from 0° to 360°, but it can never be more than 360°.
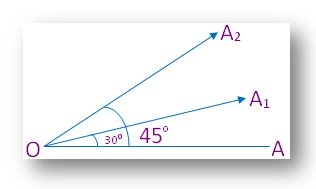 |
In fact, when a ray after rotating in any direction coincides with its initial position, then it produces an angle of 360°. In this figure, ∠AOA1 = 30°, ∠AOA2 = 45°; naturally, ∠A1OA2 =15°. |
(2) In trigonometry, we not only consider the angle made by a rotating ray with its initial position, but also the direction (i.e, clockwise or anti-clockwise) in which the ray is rotating. If a ray rotates in the anticlockwise direction, then, angles produced by it are defined as positive. On the other hand, if a ray rotates in the clockwise direction, the angles thus produced are taken as negative.
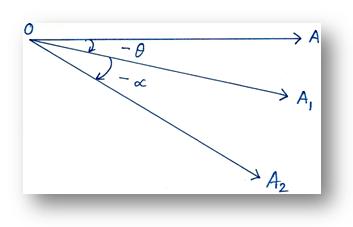 |
Again, in this figure, the ray has rotated in the clockwise direction and produced negative angles. In this case ∠AOA1 = - θ & and ∠AOA2 = -α. |
Now we shall discuss if a rotating ray after completing a full revolution further rotates through some angles, then how the angle finally produced is measured.
In case of geometric angles, if a ray completes a full revolution and coincides with its initial position, then it makes an angle of 360°. Now if it further starts to rotate, then the angle is again measured afresh from 0°. The angle will never be more than 360°. Here, we again mention that in case of geometric angles we do not take into consideration whether the ray is rotating in clockwise or anti-clockwise direction.
A trigonometric angle starting from 0° can assume any value, even it can be negative. The number of times a ray makes a complete revolution in the anticlockwise direction from its initial position, say an angle θ, the number of times the angle 360° is added to the angle θ.
Similarly, the number of times a ray makes complete revolution in the clockwise direction, the angle 360° is decreased that number of times.
 |
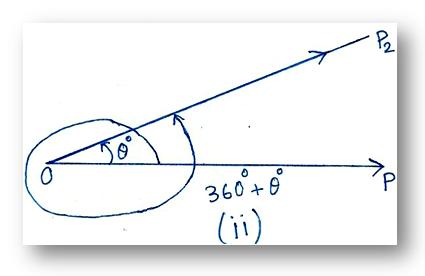 |
For example, if a ray revolves in the anticlockwise direction to make two complete revolutions and further makes an angle 30°, then the total angle formed is 2 × 360° + 30° = 750°
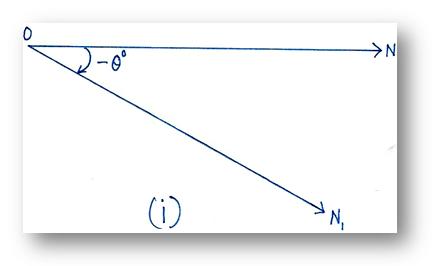
If a ray rotates in the clockwise direction, we can give analogous explanation for negative angles.
 |
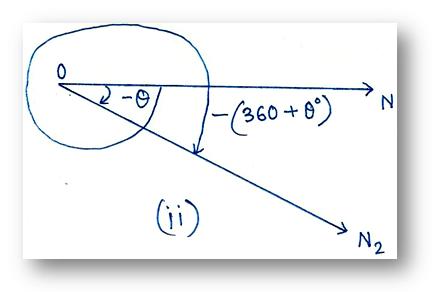 |
In this way we can explain a negative angle in trigonometry.
Basic Trigonometry
Measurement of Trigonometric Angles
Relation between Sexagesimal and Circular
Conversion from Sexagesimal to Circular System
Conversion from Circular to Sexagesimal System
From Measurement of Trigonometric Angles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.