Systems of Measuring Angles

The following three different systems of units are used in the measurement of trigonometrical angles :

(a) Sexagesimal System ( or English System)

(b) Centesimal System ( or French System)

(c) Circular System

If a straight line stands on another line and if the two adjacent angles thus formed are equal to one another then by geometry, each of these angles is called a right angle. This right angle forms the basis in defining the different systems for the measurement of angles.

Definition of systems of measuring angles:

(a) Sexagesimal System: In Sexagesimal System, an angle is measured in degrees, minutes and seconds.

A complete rotation describes 360°. In this system, a right angle is divided into 90 equal parts and each such part is called a Degree (1°); a degree is divided into 60 equal parts and each such part is called a Sexagesimal Minute (1’) and a minute is further sub-divided into 60 equal parts, each of which is called a Sexagesimal Second (1’’). In short, 

(b) Centesimal System: In Centesimal System, an angle is measured in grades, minutes and seconds. In this system, a right angle is divided into 100

equal parts and each such part is called a Grade (1^g); again, a grade is divided into 100 equal parts and each such part is called a Centesimal Minute (1‵) ; and a minute is further sub-divided into 100 equal parts, each of which is called a Centesimal Second (1‶). In short,

Note: (i) Clearly, minute and second in sexagesimal and centesimal systems are different.

For example,

1 right angle = 90 × 60 = 5400 sexagesimal minutes = (5400)’

and 1 right angle = 100 × 100 = 10000 centesimàl minutes = (10000)‶

(ii) Since, 1 right angle = 90° = 100^g
Therefore, 90° = 100^g
or, 1° = (10/9) ^g and 1^g = (9/10)°

The first relation is used to reduce an angle of sexagesimal system to centesimal system and the second is used to reduce an angle of centesimal system to sexagesimal system.

(c) Circular System: In this System, an angle is measured in radians. In higher mathematics angles are usually measured in circular system. In this system a radian is considered as the unit for the measurement of angles.

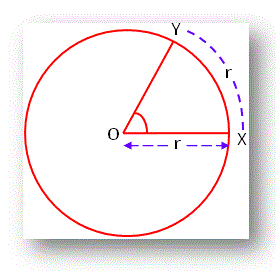
Definition of Radian: A radian is an angle subtended at the center of a circle by an arc whose length is equal to the radius.

`

A radian defined as follows:

In any circle, the angle subtended at its centre by an arc of the circle whose length is equal to the radius of the circle is called a radian. Let OX = r be the radius of a circle having center at O. Now, take an arc XY of the circle such that arc XY = r and join OY. By definition, ∠XOY = one radian. One radian is written as 1^c, 2 radians as 2^c and in general, k radians as k^c.

Circular (radian) measure of an angle:

The circular measure of an angle is the number of radians it contains.

Thus the circular (radian) measure of a right angle is π/2.

If an angle is given without mentioning units, it is assumed to be in radians. The relation between degree measures and circular (radian) measures of some standard angles are given below:

`

● Measurement of Angles

• Sign of Angles
  
• Trigonometric Angles
• Measure of Angles in Trigonometry
• Systems of Measuring Angles
• Important Properties on Circle
• S is Equal to R Theta
• Sexagesimal, Centesimal and Circular Systems
• Convert the Systems of Measuring Angles
• Convert Circular Measure
• Convert into Radian
• Problems Based on Systems of Measuring Angles
• Length of an Arc
• Problems based on S R Theta Formula

11 and 12 Grade Math

From Systems of Measuring Angles to HOME PAGE