Measure of Angles in Trigonometry
The concept of measure of angles in trigonometry is more general compared to a geometrical angle.
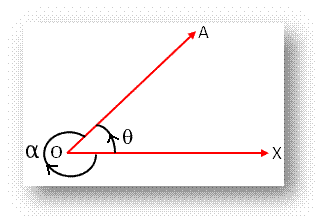
More than thousands of years ago, the ancient Babylonians chose 360 as their number to measure angles. An angle in geometry is supposed to be formed by the intersection of two lines and always varies from 0 to 360°. The unit of an angle is called a ‘degree’ (°). One full rotation indicates 360°.
A angle θ is said to be acute angle if 0° ≤ θ < 90°
A angle θ is said to be right angle if θ = 90°
A angle θ is said to be obtuse angle if 90° < θ < 180°
A angle θ is said to be straight angle if θ = 180°
A angle θ is said to be reflex angle if 180° < θ < 360°
Geometrical
angles are always positive. In other words in geometry there is no use of
negative angles. But the measure of angles in trigonometry is formed by the
revolution of a straight line about a fixed point and the magnitude of such
angle has no definite limit i.e., a
trigonometrical angle may have any positive or negative value.
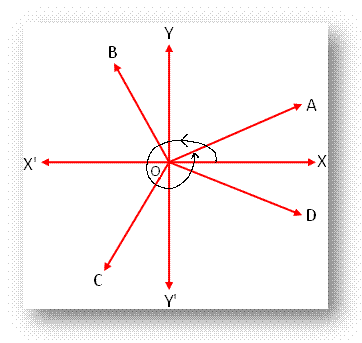
A trigonometrical angle may have any positive or negative value i.e., such an angle has no definite limit. To make the point clear we take a fixed point O on the plane of the paper and draw two mutually perpendicular lines XOX’ and YOY’ through O. Clearly, the drawn two lines divide the plane of the paper into four regions XOY , YOX‘, X ‘OY‘ and Y‘OX ; these four regions are respectively called the first, second, third and fourth quadrants. Now, assume that the generating line OA revolves about O in the anti-clockwise sense and starting from the initial position OX comes in the positions OA, OB, OC, OD describing angles ∠XOA, ∠XOB, ∠XOC and ∠XOD in the first, second, third and fourth quadrants respectively.
Clearly, each of the angles ∠XOA, ∠XOB, ∠XOC, ∠XOD is positive and 0 < ∠XOA < 90°, 90° < ∠XOB < 180°, 180° < ∠XOC < 270° and 270° < ∠XOD < 360°.
Thus, any positive angle between 0° and 360° can be described by the revolving line if it does not complete a complete revolution in the anti-clockwise sense and the angle 360° is described when it coincides with OX after a complete revolution. If OA revolves further in the same direction then an angle greater than 360° is described by it. Clearly, an angle between 360° and 720° is described by the revolving line OA if it completes one revolution but does not complete two revolutions in the anti-clockwise sense. In this way a positive angle of any given magnitude can be described by OA by its repeated revolution in the anti-clockwise sense.
For example, consider the measure of angles in trigonometry 2770°. Since 2770° = 7 × 360° + 180° + 70°, hence, angle of magnitude 2770° is described by the revolving line OA if it coincides with OC in the third quadrant after making seven complete revolutions in the anti-clockwise sense. Similarly, if the revolving line OA starts from the initial position OX and revolves about O in the clockwise sense, then negative angle of any given magnitude can be described by OA.
● Measurement of Angles
- Sign of Angles
- Trigonometric Angles
- Measure of Angles in Trigonometry
- Systems of Measuring Angles
- Important Properties on Circle
- S is Equal to R Theta
- Sexagesimal, Centesimal and Circular Systems
- Convert the Systems of Measuring Angles
- Convert Circular Measure
- Convert into Radian
- Problems Based on Systems of Measuring Angles
- Length of an Arc
- Problems based on S R Theta Formula
From Measure of Angles in Trigonometry to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.