S is Equal to R Theta

Prove that S is equal to r theta

                Or

Theta equals s over r

               Or

s r theta formula

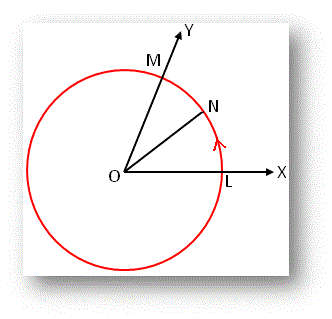
Prove that the radian measure of any angle at the centre of a circle is equal to the ratio of the arc subtending that angle at the centre to the radius of the circle.

Let, XOY be a given angle. Now, with centre O and any radius OL draw a circle.



Suppose the drawn circle intersects OX and OY at L and M respectively. Clearly, arc LM subtends ∠LOM at the centre O. Now, take an arc LN of length equal to the radius of the circle and join ON.

Then, by definition, ∠LON = 1 radian.

Since the ratio of two arcs in a circle is equal to the ratio of the angles subtended by the arcs at the center of the circle, hence,

∠LOM/∠LON = arc LM/arc LN
or, ∠LOM/1 radian = arc LM/radius OL
or, ∠LOM = arc LM/radius OL × 1 radian = arc LM/ radius OL radian.
Therefore, circular measures of ∠LOM is arc LM/radius OL
If θ be the circular measure of ∠LOM, arc LM = s and radius of the circle = OL = r then,

θ = s/r, [i.e. theta equals s over r]

or, s = r θ, [i.e. s r theta formula]

 

Therefore, now we know the meaning of “S is equal to r theta”

● Measurement of Angles

• Sign of Angles
  
• Trigonometric Angles
• Measure of Angles in Trigonometry
• Systems of Measuring Angles
• Important Properties on Circle
• S is Equal to R Theta
• Sexagesimal, Centesimal and Circular Systems
• Convert the Systems of Measuring Angles
• Convert Circular Measure
• Convert into Radian
• Problems Based on Systems of Measuring Angles
• Length of an Arc
• Problems based on S R Theta Formula

11 and 12 Grade Math

From S is Equal to R Theta to HOME PAGE