Standard Equation of an Hyperbola

We will learn how to find the standard equation of a hyperbola.

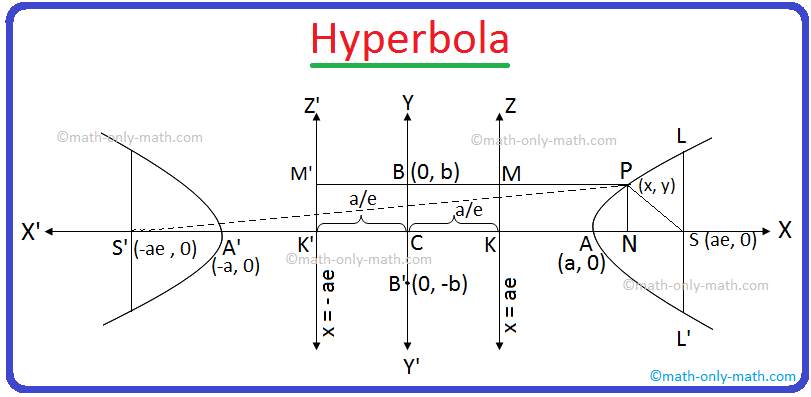
Let S be the focus, e (> 1) be the eccentricity and line KZ its directrix of the hyperbola whose equation is required.

From the point S draw SK perpendicular to the directrix KZ. The line segment SK and the produced SK divides internally at A and externally at A’ respectively in the ratio e : 1.

Then,

\(\frac{SA}{AK}\) = e : 1      

⇒ SA = e  ∙ AK …………. (ii)

and  \(\frac{SA'}{A'K}\) =  e : 1    

⇒ SA' = e  ∙ A'K …………………. (ii)

The points A and A' he on the required hyperbola because according to the definition of hyperbola A and A’are such points that their distance from the focus bear constant ratio e (>1) to their respective distance from the directrix, therefore A and A' he on the required hyperbola.

Let AA’ = 2a and C be the mid-point of the line segment AA'. Therefore, CA = CA' = a.

Now draw CY perpendicular to AA’ and mark the origin at C. CX and CY are assumed as x and y-axes respectively.

Now, adding the above two equations (i) and (ii) we have,

SA + SA' = e (AK + A'K)

⇒ CS - CA + CS + CA' =  e (AC - CK + A’C + CK)

⇒ CS - CA + CS + CA' =  e (AC - CK + A’C + CK)

Now put the value of CA = CA' = a.

⇒ CS - a + CS + a = e (a - CK + a + CK)

⇒2CS = e (2a)

⇒ 2CS = 2ae

⇒ CS = ae …………………… (iii)

Now, again subtracting above two equations (i) from (ii) we have,

⇒ SA' - SA = e (A'K - AK)

⇒ AA'= e {(CA’ + CK) - (CA - CK)}

⇒ AA' = e (CA’ + CK - CA + CK)

Now put the value of CA = CA' = a.

⇒ AA' = e (a + CK - a + CK)

⇒ 2a = e (2CK)

⇒ 2a = 2e (CK)

⇒ a = e (CK)

⇒ CK = \(\frac{a}{e}\) ………………. (iv)

Let P (x, y) be any point on the required hyperbola and from P draw PM and PN perpendicular to KZ and KX respectively. Now join SP.

According to the graph, CN = x and PN = y.

Now form the definition of hyperbola we get,

SP = e ∙ PM

⇒ Sp\(^{2}\)= e\(^{2}\)PM\(^{2}\)

⇒ SP\(^{2}\) = e\(^{2}\)KN\(^{2}\)

⇒ SP\(^{2}\) = e\(^{2}\)(CN - CK)\(^{2}\)

⇒ (x - ae)\(^{2}\) + y\(^{2}\) = e\(^{2}\)(x - \(\frac{a}{e}\))\(^{2}\), [From (iii) and (iv)]

⇒ x\(^{2}\) - 2aex + (ae)\(^{2}\) + y\(^{2}\) = (ex - a)\(^{2}\)

⇒ (ex)\(^{2}\) - 2aex + a\(^{2}\) = x\(^{2}\) - 2aex + (ae)\(^{2}\) + y\(^{2}\)

⇒ (ex)\(^{2}\)  - x\(^{2}\) - y\(^{2}\) = (ae)\(^{2}\) - a\(^{2}\)

⇒ x\(^{2}\)(e\(^{2}\) - 1) - y\(^{2}\) = a\(^{2}\)(e\(^{2}\) - 1)

⇒ \(\frac{x^{2}}{a^{2}}\) - \(\frac{y^{2}}{a^{2}(e^{2} - 1)}\) = 1

We know that a\(^{2}\)(e\(^{2}\) - 1) = b\(^{2}\)

Therefore, \(\frac{x^{2}}{a^{2}}\) - \(\frac{y^{2}}{b^{2}}\) = 1

For all the points P (x, y) the relation \(\frac{x^{2}}{a^{2}}\) - \(\frac{y^{2}}{b^{2}}\) = 1 satisfies on the required hyperbola.

Therefore, the equation \(\frac{x^{2}}{a^{2}}\) - \(\frac{y^{2}}{b^{2}}\) = 1 represents the equation of the hyperbola.

The equation of a hyperbola in the form of \(\frac{x^{2}}{a^{2}}\) - \(\frac{y^{2}}{b^{2}}\) = 1 is known as the standard equation of the hyperbola.

● The Hyperbola

• Definition of Hyperbola
• Standard Equation of an Hyperbola
  
• Vertex of the Hyperbola
• Centre of the Hyperbola
• Transverse and Conjugate Axis of the Hyperbola
• Two Foci and Two Directrices of the Hyperbola
• Latus Rectum of the Hyperbola
• Position of a Point with Respect to the Hyperbola
• Conjugate Hyperbola
• Rectangular Hyperbola
• Parametric Equation of the Hyperbola
• Hyperbola Formulae
• Problems on Hyperbola

11 and 12 Grade Math 

From Standard Equation of an Hyperbola to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit