Radian is a Constant Angle
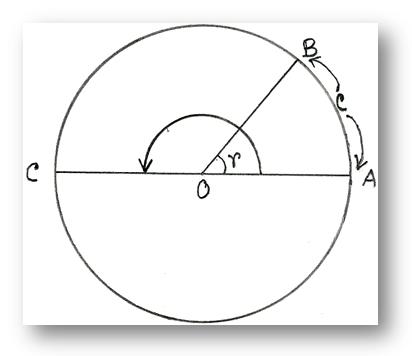
Here we will discuss about radian is a constant angle. Let O be the centre of a circle and radius OR = r. If we take an arc AB = OA = r, then by definition, ∠AOB =1 radian.
Let AO be produced to meet the circle at the point C. Then the length of the arc ABC half the circumference and ∠AOC, the angle at the centre subtended by this arc = a straight angle = two right angles.
Now if we take the ratio of the two arcs and that of the two angles, we have
arc AB/arc ABC = r/(1/2 × 2∙π∙r) = 1/ π
∠AOB/∠AOC = 1 radian/2 right angles
But in geometry, we can show that an arc of a circle is proportional to the angle it subtends at the centre of the circle.
Therefore, ∠AOB/∠AOC = arc AB/arc ABC
or, 1 radian/2 right angles = 1/π
Therefore, 1 radian = 2/π right angles
This is constant as both 2 right angles and π are constants.
The approximate value of π is taken as 22/7 for calculation
Corollary:
|
π radian = = |
2 right angles 180° |
If we express one radian in the units of sexagesimal system, we will get
|
1 radian = = = |
180°/(22/7) (180 × 7°)/22 57° 16’ 22” (approx.) |
Basic Trigonometry
Measurement of Trigonometric Angles
Relation between Sexagesimal and Circular
Conversion from Sexagesimal to Circular System
Conversion from Circular to Sexagesimal System
From Radian is a Constant Angle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Converting Fractions to Decimals | Solved Examples | Free Worksheet
Apr 28, 25 01:43 AM
In converting fractions to decimals, we know that decimals are fractions with denominators 10, 100, 1000 etc. In order to convert other fractions into decimals, we follow the following steps: -
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
Apr 27, 25 10:13 AM
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its… -
Converting Decimals to Fractions | Solved Examples | Free Worksheet
Apr 26, 25 04:56 PM
In converting decimals to fractions, we know that a decimal can always be converted into a fraction by using the following steps: Step I: Obtain the decimal. Step II: Remove the decimal points from th… -
Worksheet on Decimal Numbers | Decimals Number Concepts | Answers
Apr 26, 25 03:48 PM
Practice different types of math questions given in the worksheet on decimal numbers, these math problems will help the students to review decimals number concepts. -
Multiplication Table of 4 |Read and Write the Table of 4|4 Times Table
Apr 26, 25 01:00 PM
Repeated addition by 4’s means the multiplication table of 4. (i) When 5 candle-stands having four candles each. By repeated addition we can show 4 + 4 + 4 + 4 + 4 = 20 Then, four 5 times
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.