Math Problem Solver

Math problem solver can guide you to solve similar types of question. If you have any question which you find difficult to solve then you can fill-up the below comment box to to convey your message, so that math problem solver can help you.

1. Name the quadrant, if any, in which each point is located.

(a) (-3, 6)

(b) (7, -5)

Solution:

(a) (-3, 6) --------- II Quadrant.

(b) (7, -5) --------- IV Quadrant.

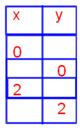
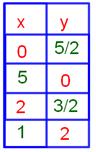
2. Complete the table for the given equation and graph the equation;

x + 2y = 5

Solution:

x + 2y = 5

Put the value of x = 0 in the equation x + 2y = 5

0 + 2y = 5

2y = 5

2y/2 = 5/2

y = 5/2

(0, 5/2)

Put the value of y = 0,

x + 2 × 0 = 5

x = 5

(5, 0)

Put the value of x = 2,

2 + 2y = 5

2 – 2 + 2y = 5 - 2

2y = 3

2y/2 = 3/2

y = 3/2

(2, 3/2)

Put the value of y = 2,

x + 2 × 2 = 5

x + 4 = 5

x + 4 – 4 = 5 – 4

x = 1

(1, 2)

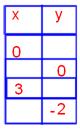
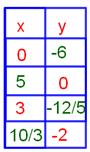
3. Complete the table for the given equation and graph the equation;

6x-5y=30

Solution:

6x-5y=30

Put the value of x = 0 in the equation 6x - 5y = 30.

6 × 0 - 5y = 30

-5y = 30

-5y/-5 = 30/-5

y = -6

(0, -6)

Put the value of y = 0,

6x - 5 × 0 = 30

6x = 30

6x/6 = 30/6

x = 5

(5, 0)

Put the value of x = 3,

6 × 3 - 5y = 30

18 - 5y = 30

18 – 18 – 5y = 30 – 18

-5y = 12

-5y/-5 = 12/-5

y= -12/5

(3, -12/5)

Put the value of y = -2,

6x – 5(-2) = 30

6x + 10 = 30

6x + 10 – 10 = 30 – 10

6x = 20

6x/6 = 20/6

x = 10/3

(10/3, -2)

4. Find the x-and y-intercepts of the following equations.

2x + 3y = 12

Solution:

2x + 3y = 12

Put the value of x = 0

2 × 0 + 3y = 12

3y = 12

3y/3 = 12/3

y = 4

Therefore, y-intercept = (0, 4)

Now, put the value of y = 0

2x + 3 × 0 = 12

2x = 12

2x/2 = 12/2

x = 6

Therefore, x-intercept = (6, 0)

5. Find the x-and y-intercepts of the following equations. x + y = -2

Solution:

x + y = -2

Put the value of x = 0

0 + y = -2

y = -2

Therefore, y-intercept = (0, -2)

Put the value of y = 0

x + 0 = -2

x = -2

Therefore, x-intercept = (-2, 0)

6. Find the midpoint of each segment with the given endpoints.

(-10, 4) and (7, 1)

Solution:

(-10, 4) and (7, 1)

Midpoint = [(x₁ + x₂)/2, (y₁ + y₂)/2]

Here, x₁ = -10, x₂ = 7, y₁= 4 and y₂ = 1

= [(-10 + 7)/2, (4 + 1)/2]

= (-3/2, 5/2)

Answer: (-3/2, 5/2)



7. Find the midpoint of each segment with the given endpoints.

(3,-6) and (6, 3)

Solution:

(3,-6) and (6, 3)

Midpoint = [(x₁ + x₂)/2, (y₁ + y₂)/2]

Here, x₁ = 3, x₂ = 6, y₁= -6 and y₂ = 3

= [(3 + 6)/2, (-6 + 3)/2]

= (9/2, -3/2)

Answer: (9/2, -3/2)

8. Decide whether the lines are parallel, perpendicular or neither.

x + 4y = 7 and 4x – y = 3

Solution:

x + 4y = 7

4y = -x + 7

y = (-1/4) x + 7

Slope of the equation x + 4y = 7 is -1/4.

Again, 4x – y = 3

y = 4x – 3

Slope of the equation 4x – y = 3 is 4.

Since multiplying both the slope of the equation = -1/4 × 4 = -1

Therefore, the given two equations are perpendicular to each other.

Answer: Perpendicular

9. The ship has coordinates (2,3) the equation of the other line is x+y=2 find the shortest distance from the ship to the line.

Solution:

x + y = 2

x + y – 2 = 0

Distance from (2, 3) to the line x + y – 2 = 0

= (2 + 3 – 2)/√(1² + 1²)

= 3/√(1 + 1)

= 3/√2

= (3 × √2)/(√2 × √2)

= (3√2)/2 units.

Answer: (3√2)/2 units



10. Covert to scientific notation 0.000000373

Solution:

0.000000373

= 3.73 × 10^-7

Answer: 3.73 × 10^-7



11. Covert to decimal notation 5.347 x 10-8

Solution:

5.347 x 10-8

= 5.347/100000000

= 0.00000005347

Answer: 0.00000005347



12. Multiply and write the result in scientific notation

(3 x 10⁵) (3 x 10³)

Solution:

(3 x 10⁵) (3 x 10³)

= 9×10^{5 + 3}

= 3 × 3 × 10⁵ × 10³ = 9 × 10⁸

Answer: 9 × 10⁸

13. Simplify: 5 - 2 [8 - (2 x 2 - 4 x 4)]

Solution:

5 - 2 [8 - (2 x 2 - 4 x 4)]

= 5 - 2 [8 - (4 - 16)]

= 5 - 2 [8 - (-12)]

= 5 - 2 [8 + 12]

= 5 - 2 [20]

= 5 – 40

= -35

Answer: -35

14. Fill in the blank:

(a) The point with coordinates (0,0) is called ........of a rectangular coordinate system.

(b) To find the x-intercept of a line, we let....equal 0 and solve for ......; to find y-intercept, we let ......equal 0 and solve for.......

Solution:

(a) The point with coordinates (0,0) is called origin of a rectangular coordinate system.

(b) To find the x-intercept of a line, we let y equal 0 and solve for x ; to find y-intercept, we let x equal 0 and solve for y .



15. Name the quadrant, if any, in which each point is located.

(a) (1, 6)

(b) (-4, -2)

Solution:

(a) (1, 6) --------- I Quadrant.

(b) (-4, -2) --------- III Quadrant.

16. A restaurant meal for a group of people cost $85 total. This amount included a 6% tax and an 18% tip, both based on the price of the food. Which equation could be used to find f, the cost of the food?

A. 85 = 1.24f         B. 85 = 0.24c         C. 85 = 1.06f + 0.18         D. 85 = f + 0.24

17. Three friends share the cost of a pizza. The base price of the pizza is p and the extra toppings cost $4.50. If each person’s share was $7.15, which equation could be used to find p, the base price of the pizza?

A. 7.15 = 3p - 4.50  

B. 7.15 = 1/3(p + 4.50) 

C. 7.15 = 1/3p + 4.50

D. 7.15 = 3(p + 4.50)

Answer: B. 7.15 = 1/3(p + 4.50)

18. A tile setter is joining the angles of two tiles, A and B, to make a 90-degree angle. The degree measure of Angle A can be represented as 3y + 2 and of Angle B as 5y. Which equation represents this situation?

A. 90 = 3y +2 – 5y     B. 3y + 2 = 90 + 5y     C. 90 = 8y + 2     D. 5y + 2 = 90 + 3y

Answer: C. 90 = 8y + 2

19. One-fourth of the distance between two cities is 100 miles less than two-thirds the distance between the cities. Which equation expresses this situation?

1/4d - 100 = 2/3d ,

1/4d = 2/3d -100,

1/4d = 2/3d +100,

1/4d - 2/3d = 100

Answer: 1/4d = 2/3d -100

20. What value of b makes the equation that follows true?

x² + bx – 35 = (x + 5)(x – 7)

A. -2        B. 12       C. 2       D. -12

Answer: A. -2 

`

● Math Questions Answers
● Help with Math Problems
● Answer Math Problems
● Math Problem Solver
● Math Unsolved Questions
● Math Questions
● Math Word Problems
● Word Problems on Speed Distance Time
● Algebra Word Problems – Money

Math Problem Answers Index

From Math Problem Solver to HOME PAGE