Subscribe to our βΆοΈ YouTube channel π΄ for the latest videos, updates, and tips.
Disjoint of Sets using Venn Diagram
Disjoint of sets using Venn diagram is shown by two non-overlapping closed regions and said inclusions are shown by showing one closed curve lying entirely within another.
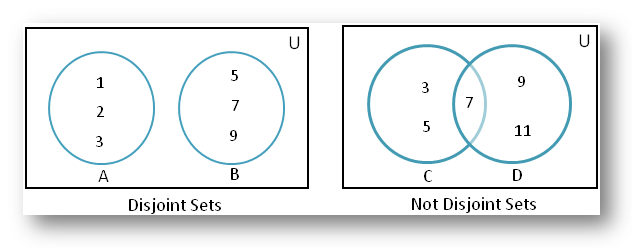
Two sets A and B are said to be disjoint, if they have no element in common.
Thus, A = {1, 2, 3} and B = {5, 7, 9} are disjoint sets; but the sets C = {3, 5, 7} and D = {7, 9, 11} are not disjoint; for, 7 is the common element of A and B.
Two sets A and B are said to be disjoint, if A β© B = Ο. If A β© B β Ο, then A
and B are said to be intersecting or overlapping sets.
Examples to show disjoint of sets using Venn diagram:
1.
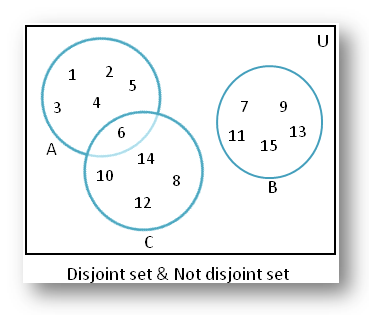
If A = {1, 2, 3, 4, 5, 6}, B = {7, 9, 11, 13, 15} and C = {6, 8, 10, 12, 14} then A and B are disjoint sets since they have no element in common while A and C are intersecting sets since 6 is the common element in both.
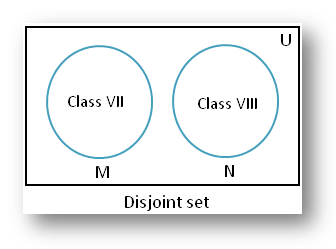
2. (i) Let M = Set of students of class VII
And N = Set of students of class VIII
Since no student can be common to both the classes; therefore set M and set N are disjoint.
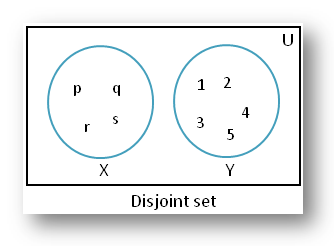
(ii) X = {p, q, r, s} and Y = {1, 2, 3, 4, 5}
Clearly, set X and set Y have no element common to both; therefore set X and set Y are disjoint sets.
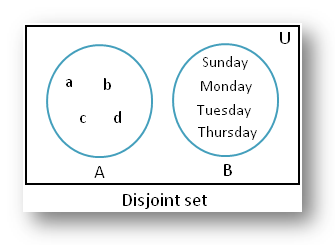
3.
A = {a, b, c, d} and B = {Sunday, Monday, Tuesday, Thursday} are disjoint because they have no element in common.
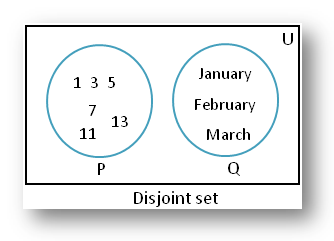
4.
P = {1, 3, 5, 7, 11, 13} and Q = {January, February, March} are disjoint because they have no element in common.
Note:
1. Intersection of two disjoint sets is always the empty set.
2. In each Venn diagram βͺ is the universal set and A, B and C are the sub-sets of βͺ.
β Set Theory
β Sets Theory
β Types of Sets
β Finite Sets and Infinite Sets
β Power Set
β Problems on Intersection of Sets
β Problems on Complement of a Set
β Problems on Operation on Sets
β Venn Diagrams in Different Situations
β Relationship in Sets using Venn Diagram
β Union of Sets using Venn Diagram
β Intersection of Sets using Venn Diagram
β Disjoint of Sets using Venn Diagram
β Difference of Sets using Venn Diagram
8th Grade Math Practice
From Disjoint of Sets using Venn Diagram to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.