Definition of Hyperbola

We will discuss the definition of hyperbola and how to find the equation of the hyperbola whose focus, directrix and eccentricity are given.

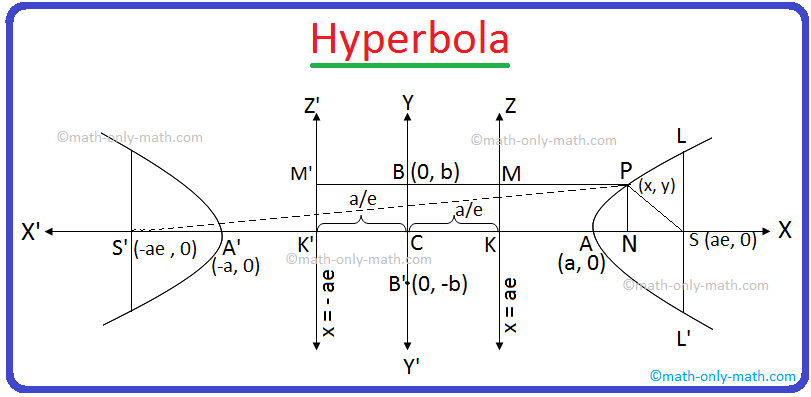
If a point (P) moves in the plane in such a way that the ratio of its distance from a fixed point (S is known as focus) in the same plane to its perpendicular distance from the fixed line (L is known as dirctrix) is always constant which is always greater than unity, then the locus traced out by P is called a Hyperbola.

Let S and L be a fixed point and a fixed straight line on a plane respectively. If the point P moves on this plane in such a way that its distance from the fixed point S always constant ratio to its perpendicular distance from the fixed line L and its ratio is greater than unity then the locus of the point P is called a Hyperbola.

The fixed point S is called a focus and the fixed straight line L, the corresponding directrix and the constant ratio is called the eccentricity of the hyperbola. The eccentricity is generally denoted by e (> 1).

If S is the focus, Z is the directrix and P is any point on the hyperbola, then by definition

$\frac{SP}{PM}$ = e

⇒ SP = e ∙ PM

Solved example to find the equation of the hyperbola whose focus, directrix and eccentricity are given:

The equation of the directrix of a hyperbola is x + y = -1. Its focus is at (1, 2) and the eccentricity is $\frac{3}{2}$. Find the equation of the hyperbola.

Solution:

Let P(x, y) be any point on the required hyperbola. If PM is the length of the perpendicular from P upon the directrix  x + y = -1 or, x + y + 1 = 0 then

PM = $\frac{x + y + 1}{\sqrt{1^{2} + (-1)^{2}}}$ =  $\frac{x + y + 1}{√2}$        

Again, the distance of P from the focus S (- 1, 1) is

SP = $\sqrt{(x - 1)^2 + (y - 1)^2}$

Since the point Plies on the required hyperbola, hence by definition we have,

$\frac{SP}{PM}$ = e

SP = e ∙ PM

⇒ SP$^{2}$ = e$^{2}$(PM)$^{2}$

⇒ (x - 1)$^{2}$ + (y - 2)$^{2}$ = $\frac{9}{4}$ $\frac{(x + y + 1)^{2}}{2}$, [Since, e = 3]

⇒ 8x$^{2}$ + 8y$^{2}$ - 16x - 32y + 40 = 9x$^{2}$ + 9y$^{2}$ + 9 + 18xy + 18x + 18y

⇒ x$^{2}$ + y$^{2}$ + 18xy + 34x + 50y - 31 = 0, which is the required equation of the hyperbola.

● The Hyperbola

• Definition of Hyperbola
• Standard Equation of an Hyperbola
  
• Vertex of the Hyperbola
• Centre of the Hyperbola
• Transverse and Conjugate Axis of the Hyperbola
• Two Foci and Two Directrices of the Hyperbola
• Latus Rectum of the Hyperbola
• Position of a Point with Respect to the Hyperbola
• Conjugate Hyperbola
• Rectangular Hyperbola
• Parametric Equation of the Hyperbola
• Hyperbola Formulae
• Problems on Hyperbola

11 and 12 Grade Math 

From Definition of Hyperbola to HOME PAGE