Venn Diagrams

Venn diagrams are useful in solving simple logical problems. Let us study about them in detail. Mathematician John Venn introduced the concept of representing the sets pictorially by means of closed geometrical figures called Venn diagrams. In Venn diagrams, the Universal Set ξ is represented by a rectangle and all other sets under consideration by circles within the rectangle. In this chapter, we will use Venn diagrams to illustrate various operations (union, intersection, difference).

What are Venn Diagrams?

Pictorial representations of sets represented by closed figures are called set diagrams or Venn diagrams. 

Venn diagrams are used to illustrate various operations like union, intersection and difference. 

We can express the relationship among sets through this in a more significant way. 

In this, 

• A rectangle is used to represent a universal set.

• Circles or ovals are used to represent other subsets of the universal set.

Venn diagrams in different situations

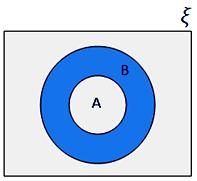
• If a set A is a subset of set B, then the circle representing set A is drawn inside the circle representing set B.

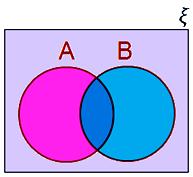
• If set A and set B have some elements in common, then to represent them, we draw two circles which are overlapping.

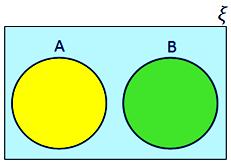
• If set A and set B are disjoint, then they are represented by two non-intersecting circles.

In this diagrams, the universal set is represented by a rectangular region and its subsets by circles inside the rectangle. We represented disjoint set by disjoint circles and intersecting sets by intersecting circles.

● Set Theory

● Sets

● Objects Form a Set

● Elements of a Set

● Properties of Sets

● Representation of a Set

● Different Notations in Sets

● Standard Sets of Numbers

● Types of Sets

● Pairs of Sets

● Subset

● Subsets of a Given Set

● Operations on Sets

● Union of Sets

● Intersection of Sets

● Difference of two Sets

● Complement of a Set

● Cardinal number of a set

● Cardinal Properties of Sets

7th Grade Math Problems

From Venn Diagrams to HOME PAGE