Cardinal Properties of Sets

Cardinal Properties of Sets:

We have already learnt about the union, intersection and difference of sets. Now, we will go through some practical problems on sets related to everyday life.

If A and B are finite sets, then

• n(A ∪ B) = n(A) + n(B) - n(A ∩ B) 

If A ∩ B = ф , then n(A ∪ B) = n(A) + n(B) 

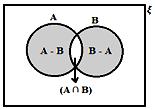
It is also clear from the Venn diagram that 

• n(A - B) = n(A) - n(A ∩ B) 

• n(B - A) = n(B) - n(A ∩ B) 

Problems on Cardinal Properties of Sets

1. If P and Q are two sets such that P ∪ Q has 40 elements, P has 22 elements and Q has 28 elements, how many elements does P ∩ Q have?

Solution: 

Given n(P ∪ Q) = 40, n(P) = 18, n(Q) = 22 

We know that n(P U Q) = n(P) + n(Q) - n(P ∩ Q) 

So, 40 = 22 + 28 - n(P ∩ Q) 

40 = 50 - n(P ∩ Q) 

Therefore, n(P ∩ Q) = 50 – 40 

= 10 

2. In a class of 40 students, 15 like to play cricket and football and 20 like to play cricket. How many like to play football only but not cricket?

Solution:

Let C = Students who like cricket 

F = Students who like football 

C ∩ F = Students who like cricket and football both 

C - F = Students who like cricket only 

F - C = Students who like football only.

n(C) = 20     n(C ∩ F) = 15     n (C U F) = 40     n (F) = ? 

n(C ∪ F) = n(C) + n(F) - n(C ∩ F) 

40 = 20 + n(F) - 15

40 = 5 + n(F) 

40 – 5 = n(F) 

Therefore, n(F)= 35 

Therefore, n(F - C) = n(F) - n (C ∩ F) 

= 35 – 15 

= 20 

Therefore, Number of students who like football only but not cricket = 20

More problems on cardinal properties of sets

3. There is a group of 80 persons who can drive scooter or car or both. Out of these, 35 can drive scooter and 60 can drive car. Find how many can drive both scooter and car? How many can drive scooter only? How many can drive car only?

Solution:

Let S = {Persons who drive scooter}

     C = {Persons who drive car}

Given, n(S ∪ C) = 80     n(S) = 35     n(C) = 60

Therefore, n(S ∪ C) = n(S) + n(C) - n(S ∩ C)

80 = 35 + 60 - n(S ∩ C)

80 = 95 - n(S ∩ C)

Therefore, n(S∩C) = 95 – 80 = 15

Therefore, 15 persons drive both scooter and car.

Therefore, the number of persons who drive a scooter only = n(S) - n(S ∩ C)

                                                                                      = 35 – 15

                                                                                      = 20

Also, the number of persons who drive car only = n(C) - n(S ∩ C)

                                                                     = 60 - 15

                                                                     = 45

4. It was found that out of 45 girls, 10 joined singing but not dancing and 24 joined singing. How many joined dancing but not singing? How many joined both?


Solution:

Let S = {Girls who joined singing}

     D = {Girls who joined dancing}

Number of girls who joined dancing but not singing = Total number of girls - Number of girls who joined singing

45 – 24

= 21

Now, n(S - D) = 10       n(S) =24

Therefore, n(S - D) = n(S) - n(S ∩ D)

           ⇒ n(S ∩ D) = n(S) - n(S - D)

                           = 24 - 10

                           = 14

Therefore, number of girls who joined both singing and dancing is 14.

● Set Theory

● Sets

● Objects Form a Set

● Elements of a Set

● Properties of Sets

● Representation of a Set

● Different Notations in Sets

● Standard Sets of Numbers

● Types of Sets

● Pairs of Sets

● Subset

● Subsets of a Given Set

● Operations on Sets

● Union of Sets

● Intersection of Sets

● Difference of two Sets

● Complement of a Set

● Cardinal number of a set

● Cardinal Properties of Sets

● Venn Diagrams

7th Grade Math Problems

From Cardinal Properties of Sets to HOME PAGE