Elimination Method

Follow the steps to solve the system of linear equations by using the elimination method:

(i) Multiply the given equation by suitable constant so as to make the coefficients of the variable to be eliminated equal.

(ii) Add the new equations obtained if the terms having the same coefficient are opposite signs and subtract if they are of the same sign.

(iii) Solve the equation thus obtained.

(iv) Substitute the value found in any one the given equations.

(v) Solve it to get the value of the other variable.

Worked-out examples on elimination method:

1. Solve the system of equation 2x + y = -4 and 5x – 3y = 1 by the method of elimination.

Solution: 

The given equations are: 

2x + y = -4       …………… (i) 

5x – 3y = 1       …………… (ii) 

Multiply equation (i) by 3, we get; 

{2x + y = -4} …………… {× 3}

6x + 3y = -12       …………… (iii) 

Adding (ii) and (iii), we get; 

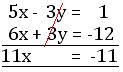
or, x = -11/11

or, x = -1

Substituting the value of x = -1 in equation (i), we get;

2 × (-1) + y = -4

-2 + y = -4

-2 + 2 + y = -4 + 2

y = -4 + 2

y = -2

Therefore, x = -1 and y = -2 is the solution of the system of equations 2x + y = -4 and 5x – 3y = 1

2. Solve the system of equation 2x + 3y = 11, x + 2y = 7 by the method of elimination.

Solution:

The given equations are:

2x + 3y = 11       …………… (i)

x + 2y = 7       …………… (ii)

Multiply the equation (ii) by 2, we get

{x + 2y = 7}       …………… (× 2)

2x + 4y = 14       …………… (iii)

Subtract equation (i) and (ii), we get

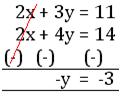
Substituting the value of y = 3 in equation (i), we get 

2x + 3y = 11 

or, 2x + 3 × 3 = 11

or, 2x + 9 = 11

or, 2x + 9 – 9 = 11 – 9

or, 2x = 11 – 9

or, 2x = 2 

or, x = 2/2 

or, x = 1

Therefore, x = 1 and y = 3 is the solution of the system of the given equations. 

3. Solve 2a – \(\frac{3}{b}\) = 12 and 5a + \(\frac{7}{b}\) = 1

Solution:

The given equations are:

2a – \(\frac{3}{b}\) = 12       …………… (i)

5a + \(\frac{7}{b}\) = 1        …………… (ii)

Put \(\frac{1}{b}\)  = c, we have

2a – 3c = 12       …………… (iii)

5a + 7c = 1         …………… (iv)

Multiply equation (iii) by 5 and (iv) by 2, we get

10a – 15c = 60       …………… (v)

10a + 14c = 2        …………… (vi)

Subtracting (v) and (vi), we get

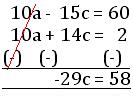
or, c = \(\frac{58}{-29}\)

or, c = -2

But \(\frac{1}{b}\) = c

Therefore, \(\frac{1}{b}\) = -2 or b = -\(\frac{1}{2}\)

Subtracting the value of c in equation (v), we get

10a – 15 × (-2) = 60

or, 10a + 30 = 60

or, 10a + 30 - 30= 60 - 30

or, 10a = 60 – 30

or, a = \(\frac{30}{10}\)

or, a = 3

Therefore, a = 3 and b = - \(\frac{1}{2}\) is the solution of the given system of equations.

4. x/2 + 2/3 y = -1 and x – 1/3 y = 3

Solution:

The given equations are:

x/2 + 2/3 y = -1       …………… (i)

x – 1/3 y = 3       …………… (ii)

Multiply equation (i) by 6 and (ii) by 3, we get;

3x + 4y = -6       …………… (iii)

3x – y = 9       …………… (iv)

Solving (iii) and (iv), we get;

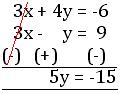
or, y = -15/5

or, y = -3

Subtracting the value of y in (ii), we get;

x - 1/3̶ × -3̶ = 3

or, x + 1 = 3

or, x = 3 – 1

or, x = 2

Therefore, x = 2 and y = -3 is the solution of the equation.

x/2 + 2/3 y = -1 and x - y/3 = 3

● Simultaneous Linear Equations

Simultaneous Linear Equations

Comparison Method

Elimination Method

Substitution Method

Cross-Multiplication Method

Solvability of Linear Simultaneous Equations

Pairs of Equations

Word Problems on Simultaneous Linear Equations

Word Problems on Simultaneous Linear Equations

Practice Test on Word Problems Involving Simultaneous Linear Equations

● Simultaneous Linear Equations - Worksheets

Worksheet on Simultaneous Linear Equations

Worksheet on Problems on Simultaneous Linear Equations

8th Grade Math Practice 

From Elimination Method to HOME PAGE