Cube

If a number is multiplied by itself three times, then the product is called the cube of that number.

To denote the cube of a number, 3 is written a little up to the right of the numbers.

Thus, 3 is the power of x and is read as “x cubed”.

Cube of a number:

When a number is multiplied three times by itself, the product obtained is called the cube of a number.

For a given numberm, we define, cube of m = m × m × m, denoted by m³.

For example:

(i) 2³ = (2 × 2 × 2) = 8.

Thus, cube of 2 is 8.

(ii) 3³ = (3 × 3 × 3) = 27.

Thus, cube of 3 is 27.

(iii) 4 × 4 × 4 = 64, here 64 is the cube of 4.

(iv) 5 × 5 × 5 = 125, here 125 is the cube of 5.

Perfect cube:

A natural number (n) is said to be a perfect cube if (n = m³) it is the cube of some natural number.

For example:

1³ =1,

2³ = 8,

3³ =27,

4³ =64,

5³ =125, etc.

Thus 1, 8, 27, 64, 125, etc. are perfect cubes.


A given natural number is a perfect cube if it can be expressed as the product of triplets of equal factors.

Cubes of negative integer:

The cube of a negative integer is always negative.

For example:

(-1)³ = (-1) × (-1) × (-1) = -1,

(-2)³ = (-2) × (-2) × (-2) = -8

(-3)³ = (-3) × (-3) × (-3) = -27, etc.

Cube of a rational number:

We have, (a/b) ³ = a/b × a/b × a/b = (a × a × a)/(b × b × b) = a³/b³

Hence, (a/b) ³ = a³/ b³

For example:

(i) (3/5) ³ = 3³/5 ³ = (3 × 3 × 3)/(5 × 5 × 5) = 27/125

(ii) (-2/3) ³ = (-2) ³/ 3³ = {(-2) × (-2) × (-2)}/(3 × 3 × 3) = -8/27

Properties of cubes of numbers:

(i) The cube of every even natural number is even.

(ii) The cube of every odd natural number is odd.

Solved example to find perfect cubes step by step;

1. Show that 189 is not a perfect cube.

Solution:

Resolving 189 into prime factors, we get:

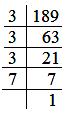
189 = 3 × 3 × 3 × 7

Making triplets, we find that one triplet is formed and we are left with one more factor.

Thus, 189 cannot be expressed as a product of triplets.

Hence, 189 is not a perfect cube.

2. Show that 216 is a perfect cube. Find the number whose cube is 216. 

Solution: 

Resolving 216 into prime factors, we get: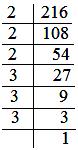 

216 = 2 × 2 × 2 × 3 × 3 × 3 = (2 × 3) × (2 × 3) × (2 × 3)

= (6 × 6 × 6)

= 6³

Thus, 216 is a perfect cube.

And, 6 is the number whose cube is 216.

3. What is the smallest number by which 3087 may be multiplied so that the product is a perfect cube?

Solution:

Writing 3087 as a product of prime factors, we have:

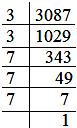
3087 = 3 × 3 × 7 × 7 × 7

Hence, to make it a perfect cube, it must be multiplied by 3.

4. What is the smallest number by which 392 may be divided so that the quotient is a perfect cube?

Solution:

Writing 392 as a product of prime factors, we have:

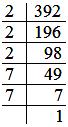
392 = 2 × 2 × 2 × 7 × 7

Clearly, to make it a perfect cube, it must be divided by (7 × 7), i.e., 49.

5. Find the cube of each of the following :

(i) (-70 )          (ii) 1²/₃          (iii) 2.5          (iv) 0.06

Solution:

(i) (-7)³

= (-7) × (-7) × (-7)

= -343


(ii) (1²/₃)³

= (5/3) ³

= 5³/3³

= (5 × 5 × 5)/(3 × 3 × 3)

= 125/27


(iii) (2.5)³

= (25/10)³

= (5/2)³

= 5³/3³

= (5× 5 × 5)/(3× 3× 3)

= 125/27



(iv) (0.06) ³

= (6/100)³

= (3/50)³ = 3³/(50)³

= (3 × 3 × 3)/(50 × 50 × 50)

= 27/125000

● Cube and Cube Roots

Cube

To Find if the Given Number is a Perfect Cube

Cube Root

Method for Finding the Cube of a Two-Digit Number

Table of Cube Roots

● Cube and Cube Roots - Worksheets

Worksheet on Cube

Worksheet on Cube and Cube Root

Worksheet on Cube Root

8th Grade Math Practice

From Cube to HOME PAGE