Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Method for Finding the Cube of a Two-Digit Number
We will learn the short-cut method for finding the cube of a two-digit number.
Suppose, we have (a + b)³ = a³ + 3a²b + 3ab² + b³.
METHOD:
For finding the cube of a two-digit number with the tens digit = a
and the units digit = b, we make four columns, headed by
a³, (3a² × b), (3a × b²) and b³
The rest of the procedure is the same as followed in squaring a number by the column method.
We simplify the working as;
a² × a = a³;
a² × 3b = 3a²b;
b² × 3a = 3ab²;
b² × b = b³;
Examples on the method for finding the cube of a two-digit number:
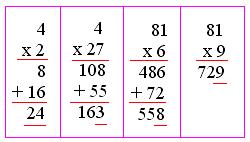
1. Find the value of (29)³ by the short-cut method.
Solution:
Here, a = 2 and b =9.
a² × a = a³;
a² × 3b = 3a² × b;
b² × 3a = 3a × b²;
b² × b = b³
Therefore, (29)³ = 24389
2. Find the value of (71)³ by the short-cut method.
Solution:
Here, a = 7 and b = 1
a² × a = a³;
a² × 3b = 3a² × b;
b² × 3a = 3a × b²;
b² × b = b³
Therefore, (71)³ = 357911
By following the above examples on the method for finding the cube of a two-digit number; we can try to find the value of each of the following using the short-cut method;
1. (25)³
2. (47)³
3. (68)³
4. (84)³
● Cube and Cube Roots
To Find if the Given Number is a Perfect Cube
Method for Finding the Cube of a Two-Digit Number
● Cube and Cube Roots - Worksheets
Worksheet on Cube and Cube Root
8th Grade Math Practice
From Method for Finding the Cube of a Two-Digit Number to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
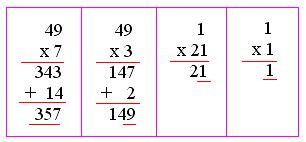


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.