Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Worksheet on Inverse Variation Using Method of Proportion
Practice the questions given in the worksheet on inverse variation using method of proportion.
We know, in inverse variation if one increases, the other decreases and if one decreases, the other increases.
In inverse variation: a1a2=b2b1
or, a1×b1=a2×b2.
For example of inverse variation:
● More labours at work, less time taken to complete the work.
Less labours at work, more time taken to complete the work.
Read the questions carefully to solve different types
of problems based on inverse variation using method of proportion. Click here
to know or learn more about
these problems.
1. 8 potters can make 96 pots in 4 days. How many potters will be needed to make 108 pots in 6 days?
2. If 5 men can build a wall in 6 days. In how many days 10 men will do it?
3. There are 124 students in the hostel. Food provision for them is for 28 days. How many more students joined the hostel so that the food lasted for 16 days?
4. A car takes 5 hours to complete a journey if it moves with a speed of 90 km/hr. How long will it take when the car travels at a speed of 75 km/hr?
5. A train moves at a speed of 110 km/hr and covers a certain distance in 9.6 hours. What should be the speed of the train to cover the same distance in 8 hours?
6. 12 men can paint the wall in 8 hours. How many men will paint the wall in 6 hours?
7. If 24 horses can graze a field in 10 days. Then how many horses will graze the same field in 15 days.
Answers for the worksheet on inverse variation using method of proportion are given below to check the exact answers of the above problems.
Answers:
1. 6 potters
2. 3 days
3. 93
4. 6 hours
5. 132 km/h
6. 16 men
7. 16 horses
Worksheet on Direct Variation using Unitary Method
Worksheet on Direct variation using Method of Proportion
Worksheet on Word Problems on Unitary Method
Worksheet on Inverse Variation Using Unitary Method
Worksheet on Inverse Variation Using Method of Proportion
7th Grade Math Problems
Math Homework Sheets
From Worksheet on Inverse Variation Using Method of Proportion to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Area, Perimeter and Volume | Square, Rectangle, Cube,Cubo
Jul 25, 25 12:21 PM
In this worksheet on area perimeter and volume you will get different types of questions on find the perimeter of a rectangle, find the perimeter of a square, find the area of a rectangle, find the ar… -
Worksheet on Volume of a Cube and Cuboid |The Volume of a RectangleBox
Jul 25, 25 03:15 AM
We will practice the questions given in the worksheet on volume of a cube and cuboid. We know the volume of an object is the amount of space occupied by the object.1. Fill in the blanks: -
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 24, 25 03:46 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
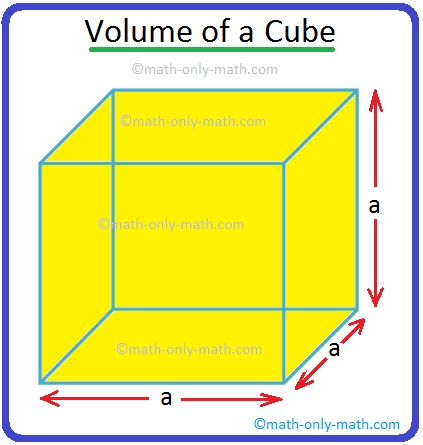
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 23, 25 11:37 AM
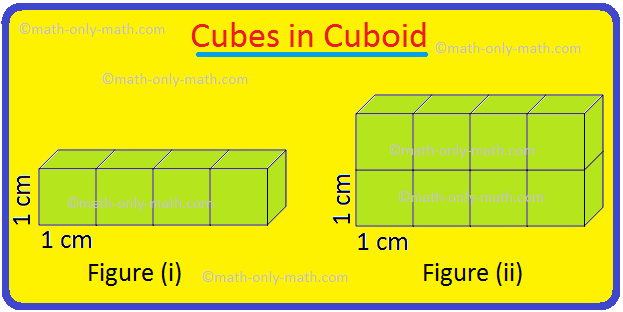
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on…
Situations of Direct Variation
Situations of Inverse Variation
Direct Variations Using Unitary Method
Direct Variations Using Method of Proportion
Inverse Variation Using Unitary Method
Inverse Variation Using Method of Proportion
Problems on Unitary Method using Direct Variation
Problems on Unitary Method Using Inverse Variation
Mixed Problems Using Unitary Method


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.