Sum of the Cubes of First n Natural Numbers
We will discuss here how to find the sum of the cubes of first n natural numbers.
Let us assume the required sum = S
Therefore, S = 1\(^{3}\) + 2\(^{3}\) + 3\(^{3}\) + 4\(^{3}\) + 5\(^{3}\) + ................... + n\(^{3}\)
Now, we will use the below identity to find the value of S:
n\(^{4}\) - (n - 1)\(^{4}\) = 4n\(^{3}\) - 6n\(^{2}\) + 4n - 1
Substituting, n = 1, 2, 3, 4, 5, ............., n in the above identity, we get
1\(^{4}\) - 0\(^{4}\) = 4 ∙ 1\(^{3}\) - 6 ∙ 1\(^{2}\) + 4 ∙ 1 - 1
2\(^{4}\) - 1\(^{4}\) = 4 ∙ 2\(^{3}\) - 6 ∙ 2\(^{2}\) + 4 ∙ 2 - 1
3\(^{4}\) - 2\(^{4}\) = 4 ∙ 3\(^{3}\) - 6 ∙ 3\(^{2}\) + 4 ∙ 3 - 1
4\(^{4}\) - 3\(^{4}\) = 4 ∙ 4\(^{3}\) - 6 ∙ 4\(^{2}\) + 4 ∙ 4 - 1
........ .................... ...............
n\(^{4}\) - (n - 1)\(^{4}\) = 4 . n\(^{3}\) - 6 ∙ n\(^{2}\) + 4 ∙ n - 1
Adding we get, n\(^{4}\) - 0\(^{4}\) = 4(1\(^{3}\) + 2\(^{3}\) + 3\(^{3}\) + 4\(^{3}\) + ........... + n\(^{3}\)) - 6(1\(^{2}\) + 2\(^{2}\) + 3\(^{2}\) + 4\(^{2}\) + ........ + n\(^{2}\)) + 4(1 + 2 + 3 + 4 + ........ + n) - (1 + 1 + 1 + 1 + ......... n times)
⇒ n\(^{4}\) = 4S - 6 ∙ \(\frac{n(n + 1)(2n + 1)}{6}\) + 4 ∙ \(\frac{n(n + 1)}{2}\) - n
⇒ 4S = n\(^{4}\) + n(n + 1)(2n + 1) - 2n(n + 1) + n
⇒ 4S = n\(^{4}\) + n(2n\(^{2}\) + 3n + 1) – 2n\(^{2}\) - 2n + n
⇒ 4S = n\(^{4}\) + 2n\(^{3}\) + 3n\(^{2}\) + n - 2n\(^{2}\) - 2n + n
⇒ 4S = n\(^{4}\) + 2n\(^{3}\) + n\(^{2}\)
⇒ 4S = n\(^{2}\)(n\(^{2}\) + 2n + 1)
⇒ 4S = n\(^{2}\)(n + 1)\(^{2}\)
Therefore, S = \(\frac{n^{2}(n + 1)^{2}}{4}\) = {\(\frac{n(n + 1)}{2}\)}\(^{2}\) = (Sum of the first n natural numbers)\(^{2}\)
i.e., 1\(^{3}\) + 2\(^{3}\) + 3\(^{3}\) + 4\(^{3}\) + 5\(^{3}\) + ................... + n\(^{3}\) = {\(\frac{n(n + 1)}{2}\)}\(^{2}\)
Thus, the sum of the cubes of first n natural numbers = {\(\frac{n(n + 1)}{2}\)}\(^{2}\)
Solved examples to find the sum of the cubes of first n natural numbers:
1. Find the sum of the cubes of first 12 natural numbers.
Solution:
Sum of the cubes of first 12 natural numbers
i.e., 1\(^{3}\) + 2\(^{3}\) + 3\(^{3}\) + 4\(^{3}\) + 5\(^{3}\) + ................... + 12\(^{3}\)
We know the sum of the cubes of first n natural numbers (S) = {\(\frac{n(n + 1)}{2}\)}\(^{2}\)
Here n = 12
Therefore, the sum of the cubes of first 12 natural numbers = {\(\frac{12(12 + 1)}{2}\)}\(^{2}\)
= {\(\frac{12 × 13}{2}\)}\(^{2}\)
= {6 × 13}\(^{2}\)
= (78)\(^{2}\)
= 6084
2. Find the sum of the cubes of first 25 natural numbers.
Solution:
Sum of the cubes of first 25 natural numbers
i.e., 1\(^{3}\) + 2\(^{3}\) + 3\(^{3}\) + 4\(^{3}\) + 5\(^{3}\) + ................... + 25\(^{3}\)
We know the sum of the cubes of first n natural numbers (S) = {\(\frac{n(n + 1)}{2}\)}\(^{2}\)
Here n = 25
Therefore, the sum of the cubes of first 25 natural numbers = {\(\frac{25(25 + 1)}{2}\)}\(^{2}\)
= {\(\frac{12 × 26}{2}\)}\(^{2}\)
= {25 × 13}\(^{2}\)
= (325)\(^{2}\)
= 105625
● Arithmetic Progression
- Definition of Arithmetic Progression
- General Form of an Arithmetic Progress
- Arithmetic Mean
- Sum of the First n Terms of an Arithmetic Progression
- Sum of the Cubes of First n Natural Numbers
- Sum of First n Natural Numbers
- Sum of the Squares of First n Natural Numbers
- Properties of Arithmetic Progression
- Selection of Terms in an Arithmetic Progression
- Arithmetic Progression Formulae
- Problems on Arithmetic Progression
- Problems on Sum of 'n' Terms of Arithmetic Progression
From Sum of the Cubes of First n Natural Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
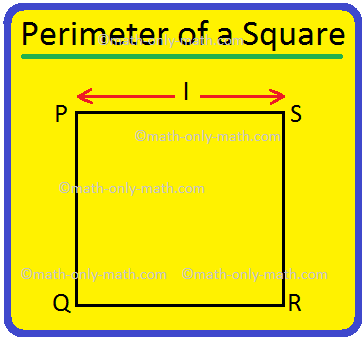
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
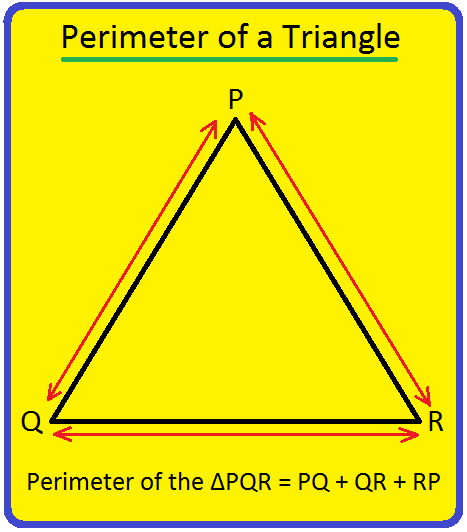
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
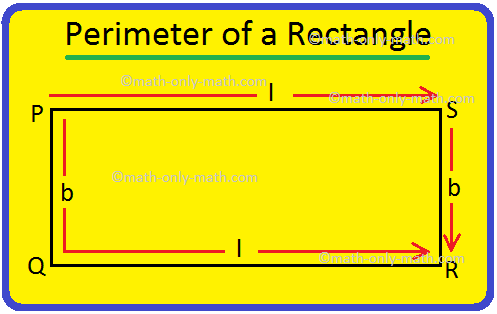
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…