Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Medians and Altitudes of a Triangle
Here we will discuss about Medians and Altitudes of a Triangle
Median of a Triangle:
The straight line joining a vertex of a triangle to the midpoint of the opposite side is called a median. A triangle has three medians. Here XL, YM and ZN are medians.
Definition of Median of a Triangle:
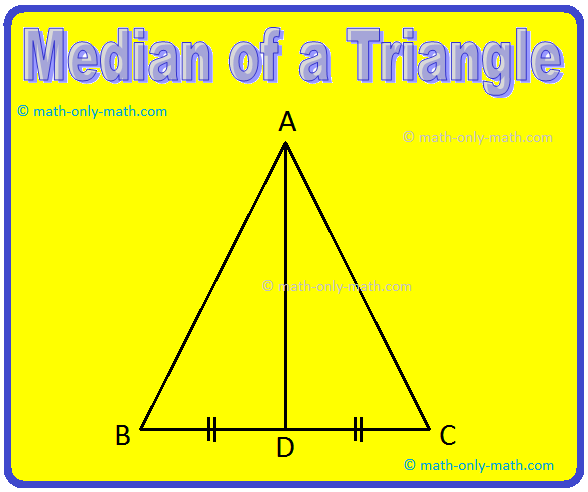
A line segment joining a vertex of a triangle to the mid-point of the opposite side is called a median of a triangle.
In the above figure, AD is a median of ∆ABC i.e., BD = DC.
A triangle has three medians.
Solved Example on Median of a Triangle:
A Geometrical Property of Medians of a Triangle:
The three medians of a triangle are concurrent, i.e., they have a common point of intersection. This point is known as the centroid of the triangle. It divides each median into the ratio 2 : 1.
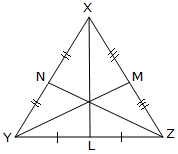
Here, the three medians intersect at G.
Thus, G is the centroid of the triangle.
Also, XG : GL = 2 : 1
YG : GM= 2 : 1
and ZG : GN = 2 : 1
Altitude of a Triangle:
Before studying altitude of a triangle, let us first know about the perpendicular lines.
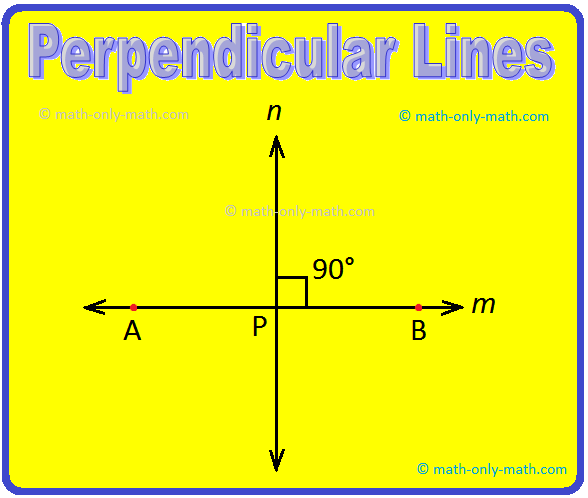
Two lines m and n are said to be perpendicular to each other, if one of the angles measured by them is a right angle. We read as n is perpendicular to m and write n ⊥ m.
Also, let P be the mid-point of AB. Then, we can say that the line n is the perpendicular bisector of the line segment AB.
REMEMBER
Two rays or two line segments are said to be perpendicular to each other, if the corresponding lines or segments determined by them are perpendicular.
For example, the foot of a table is perpendicular to the surface of the table.
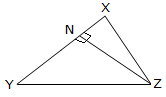
An altitude of a triangle, with respect to (or corresponding to) a side, is the perpendicular line segment drawn to the side from the opposite vertex.
Definition of a Altitude of a Triangle:
The perpendicular line drawn from vertex of a triangle to its opposite side is called an altitude.
The side on which the altitude drawn is called base.
In the adjoining figure, AL ⊥ BC. So, BC is the base and AL is the corresponding altitude of ∆ABC.
REMEMBER
There can be one perpendicular from each vertex of a triangle to the opposite side. Thus, there are three altitudes in a triangle.
Let us discuss about three altitudes in a triangle.
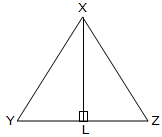
XL is the altitude with respect to the side YZ.
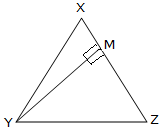
If ∆XYZ is a right-angled triangle, right angled at Y, XY is the altitude with respect to YZand YZ is the altitude with respect to XY.
If ∆XYZ is an obtuse-angled triangle in which ∠XYZ is the obtuse angle, the altitude with respect to YZ is the line segment XM drawn perpendicular to ZY produced.
Examples on Medians and Altitudes of a Triangle:
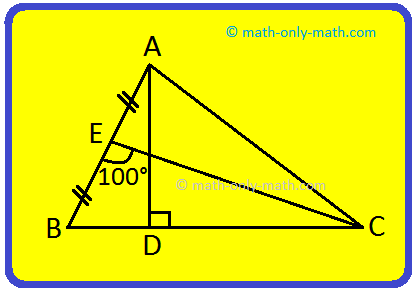
1. In the adjoining figure, name the altitude and median of ∆ABC.
Solution:
In the above figure, we find that AD ⊥ BC. Hence, AD is the altitude of AABC.
Also since CE is the bisector of AB i.e. AE = BE.
Therefore, CE is the median of ∆ABC.
From Medians and Altitudes of a Triangle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
Perimeter of a Figure | Perimeter of a Simple Closed Figure | Examples
Jul 16, 25 02:33 AM
Perimeter of a figure is explained here. Perimeter is the total length of the boundary of a closed figure. The perimeter of a simple closed figure is the sum of the measures of line-segments which hav… -
Formation of Numbers | Smallest and Greatest Number| Number Formation
Jul 15, 25 11:46 AM
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,


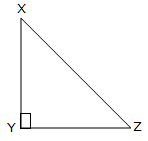
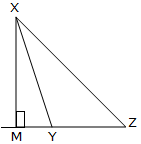











New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.