Simple Math Formula on Trigonometry

Simple math formula on trigonometry is given in such an order that students can easily get the formula.

Trigonometry

● Measurement of Trigonometrical Angles:

(i) The angle subtended at the centre of a circle by an arc whose length is equal to the radius of the circle is called a radian.

(ii) A radian is a constant angle. 

One radian = (2/π) rt. angle = 57°17’44.8” (approx.) 

(iii) 1 rt. angle = 90° ; 1° = 60’ ; 1‘ = 60”. 

(iv) 1 rt. angle = 100ᵍ ; 1ᵍ = 100’ ; 1‵ = 100‶.

(v) πᶜ 180° = 200ᵍ.

(vi) The circumference of a circle of radius r is 2πr where π is a constant; approximate value of π is ²²/₇; more accurate value of π is 3.14159 (approx.).

(vii) If Θ be the radian measure of an angle subtended at the centre of a circle of radius r by an arc of length s then Θ = ˢ/₀ or, s = rΘ.

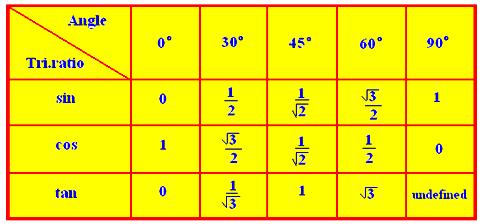
● Trigonometrical Ratios of some Standard Angles:

● Trigonometrical Ratios for Associated Angles:

(ii) If Θ is a positive acute angle and n is an even integer then,

(a) sin (n ∙ 90° ± Θ) = sin Θ or, (- sin Θ)

(b) cos (n ∙ 90° ± Θ) = cos Θ or, (- cos Θ)

(c) tan (n ∙ 90° ± Θ) = tan Θ or, (- tan Θ).

(iii) If Θ is a positive acute angle and n is an odd integer then,

(a) sin (n ∙ 90° ± Θ) = cos Θ or, (- cos Θ)

(b) cos (n ∙ 90° ± Θ) = sin Θ or, (- sin Θ)

(c) tan (n ∙ 90° ± Θ) = cot ф or (- cot Θ).

`

● Compound Angles:

(i) sin (A + B) = sin A cos B + cos A sin B.

(ii) sin ( A - B) = sin A cos B - cos A sin B.

(iii) cos (A + B) = cos A cos B + sin A sin B.

(iv) cos (A - B) = cos A cos B + sin A sin B.

(v) sin (A + B) sin (A - B) = sin² A - sin² B = cos² B - cos² A.

(vi) cos (A + B) cos (A - B) = cos² A - sin² B = cos² B - sin² A.

(vii) tan (A+ B) = (tan A + tan B)/(1 - tan A tan B).

(viii) tan (A - B) = (tan A - tan B)/(1 + tan A tan B).

(ix) cot (A + B) = (cot A cot B - 1)/(cot B + cot A).

(x) cot (A - B) = (cot A cot B + 1)/(cot B - cot A).

(xi) tan (A + B + C) = {(tan A + tan B + tan C) - (tan A tan B tan C)}/(1 - tan A tan B - tan B tan C - tan C tan A).

(xii) 2 sin A cos B = sin (A + B) + sin(A - B).

(xiii) 2 cos A sin B = sin (A + B ) - sin (A - B).

(xiv) 2 cos A cos B = cos (A + B ) + cos (A - B).

(xv) 2 sin A sin B = cos (A - B) - cos (A + B).

(xvi) sin C + sin D = 2 sin ^{(C + D)}/₂ cos ^{(C - D)}/₂.

(xvii) sin C - sin D = 2 cos ^{(C + D)}/₂ sin ^{(C - D)}/₂.

(xviii) cos C + cos D = 2 cos ^{(C + D)}/₂ cos ^{(C - D)}/₂.

(xix) cos C - cos D = 2 sin ^{(C + D)}/₂ sin ^{(C - D)}/₂.

● Multiple Angles:

(i) sin 2Θ = 2 sin Θ cos Θ.

(ii) cos 2Θ = cos² Θ - sin² Θ.

(iii) cos 2 Θ = 2 cos² Θ - 1.

(iv) cos 2Θ = 1 - 2 sin² Θ.

(v) 1 - cos2Θ = 2 cos² Θ.

(vi) 1 - cos2Θ = 2 sin² Θ.

(vii) tan² Θ = (1 - cos 2Θ)/(1 + cos 2Θ).

(viii) sin 2Θ = (2 tan Θ)/(1 + tan² Θ)

(ix) cos 2Θ = (1 - tan² Θ)/(1 + tan² Θ).

(x) tan 2Θ = (2 tan Θ)/(1 - tan² Θ).

(xi) sin 3Θ = 3 sin Θ - 4 sin³ Θ.

(xii) cos 3ф = 4 cos³ Θ - 3 cos Θ.

(xiii) tan 3Θ = (3 tan Θ - tan³ Θ)/(1 - 3 tan² Θ).

● Submultiple Angles:

(i) sin Θ = 2 sin (Θ/2) cos (Θ/2).

(ii) cos Θ = cos² (Θ/2) - sin² (Θ/2).

(iii) cos Θ = 2 cos² (Θ/2) - 1.

(iv) cos ф = 1 - 2 sin² (Θ/2).

(v) 1 + cos Θ = 2 cos² (Θ/2).

(vi) 1 - cos Θ = 2 sin² (Θ/2).

(vii) tan² (Θ/2) = (1 - cos Θ)/(1 + cos Θ).

(viii) sin Θ = [2 tan (Θ/2)]/[1 + tan² (Θ/2)].

(ix) cos Θ = [1 - tan² (Θ/2)]/[1 + tan² (Θ/2)].

(x) tan Θ = [2 tan (Θ/2)]/[1 - tan² (Θ/2)].

(xi) sin Θ = 3 sin (Θ/3) - 4 sin³ (Θ/3).

(xii) cos Θ = 4 cos³ (Θ/3) - 3 cos (Θ/2).

(xiii) (a) sin 15° = cos 75° = (√3 - 1)/(2√2).

(b) cos 15° = sin 75° = (√3 + 1)/(2√2).

(c) tan 15° = 2 - √3.

(d) sin 22 ½° = √(2 - √2).

(e) cos 22 ½° = ½ [√(2 + √2)].

(f) tan 22 ½° = √2 - 1.

(g) sin 18 ° = (√5 - 1)/4 = cos 72°.

(h) cos 36° = cos 72° = (√5 + 1)/4.

(i) cos 18° = sin 72° = ¼ [√(10 + 2√5)].

(j) sin 36° = cos 54° = ¼ [√(10 - 2√5)].

● General Solutions:

(i) (a) If sin Θ = 0 then, Θ = nπ.

(b) If sin Θ = 1 then, Θ = (4n + 1)(π/2).

(c) If sin ф = -1 then, Θ = (4n - 1)(π/2).

(d) If sin Θ = sin α then, Θ = nπ + (-1)ⁿ α.

(ii) (a) If cos Θ = 0 then, Θ = (2n + 1)(π/2).

(b) If cos Θ = 1 then, Θ = 2nπ.

(c) If cos Θ = -1 then, Θ = (2n + 1)π.

(d) If cos Θ = cos α then, Θ = 2nπ ± α.

(ii) (a) If tan Θ = 0 then, Θ = nπ.

(b) If tan Θ = tan α then, Θ = 2nπ + α where, n = 0 or any integer.

● Inverse Circular Functions:

(i) sin (sin^-1 x) = x ; cos (cos^-1 x) = x ; tan (tan^-1 x) = x.

(ii) sin^-1 (sin Θ) = Θ ; cos^-1 (cos Θ) = Θ ; tan^-1 (tan Θ) = Θ.

(iii) sin^-1 x = cosec^-1 (1/x) = cos^-1 [√(1 - x²)] = sec^-1 [1/√(1 - x²)]

= tan^-1 [x/√(1 - x²)] = cot^-1 [√(1 - x²)/x].

(iv) sin^-1 x + cos^-1 x = π/2 ; sec^-1 x + cosec^-1 x = π/2 ;

tan^-1 x + cot^-1 x = π/2.

(v) (a) tan^-1 x + tan^-1 y = tan^-1 [(x + y)/(1 - xy)]

(b) tan^-1 x - tan^-1 y = tan^-1 [(x - y)/(1 + xy)]

(vi) (a) sin^-1 x + sin^-1 y = sin^-1 {x√(1 - y²) + y√(1 - x²)}

(b) sin^-1 x - sin^-1 y = sin^-1 {x√(1 - y² ) - y√(1 - x²)}

(vii) (a) cos^-1 x + cos^-1 y = cos^-1 {xy - √(1 - x²) (1 - y²)}

(b) cos^-1 x - cos^-1 y = cos^-1 {xy + √(1 - x²) (1 - y²)}.

(viii) 2 tan^-1 x = sin^-1 [2x/(1 + x²)] = cos^-1 [(1 - x²)/(1 - x²)]

= tan^-1 [2x/(1 - x²)].

(ix) tan^-1 x + tan^-1 y + tan^-1 z = tan^-1 [(x + y + z - xyz)/(1 - xy - yz - zx)]

(x) sin^-1 x and cos^-1 x are defined when -1 ≤ x ≤ 1 ; sec^-1 x and cosec^-1 x are defined when Ι x Ι ≥ 1 ; tan^-1 x and cot^-1 x are defined
when - ∞ < x < ∞.

(xi) If principal values of sin^-1 x, cos^-1 x and tan^-1 x be α, β and γ respectively, then -π/2 ≤ α ≤ π/2, 0 ≤ β ≤ π and -π/2 ≤ γ ≤ π/2.

● Properties of Triangle:

(i) a/(sin A) = b/(sin B) = c/(sin C) = 2R.

(ii) a = b cos C + c cos B ; b = c cos A + a cos C ; c = a cos B + b cos A.

(iii) cos A = (b² + c² - a²)/2bc ; cos B = (c² + a² - b²)/2ca ;

cos C = (a² + b² - c²)/2ab

(iv) tan A = [(abc)/R] ∙[ 1/(b² + c² - a²)]

tan B = [(abc)/R] ∙ [1/(c² + a² - b²)]

tan C = [(abc)/R] ∙ [1/(a² + b² - c²)].

(v) sin (A/2) = √[(s - b) (s - c)/(bc)].

sin B/2 = √[(s - c) (s - a)/(ca)].

sin C/2 = √[(s - a) (s - b)/(ab)].

cos A/2 = √[s (s - a)/(bc)].

sin B/2 = √[s (s - b)/(ca)].

cos C/2 = √[s (s - c)/(ab)].

tan A/2 = √[(s - b) (s - c)/{s(s - c)}].

tan B/2 = √[(s - c) (s - a)/{s(s - b)}].

tan C/2 = √[(s - a) (s - b)/{s(s - c)}].

(vi) tan [(B - C)/2] = [(b - c)/(b + c)] cot (A/2).

tan [(C - A)/2] = [(c - a)/(c + a)] cot (B/2).

tan [(A - B)/2] = [(a - b)/(a + b)] cot (C/2).

(vii) ∆ = ½ [bc sin A] = ½ [ca sin B] = ½ [ab sin C].

(viii) ∆ = √{s(s - a)(s - b)(s - c)}.

(ix) R = ᵃᵇᶜ/₄₀.

(x) tan (A/2) = {(s - b)(s - c)}/∆.

tan (B/2) = {(s - c)(s - a)}/∆.

tan (C/2) = {(s - a)(s - b)}/∆

(xi) cot A/2 = {s(s - a)}/∆.

cot (B/2) = {s(s - b)}/∆.

cot (C/2) = {s(s - c)}/∆.

(xii) sin A = ^2∆/_bc ; sin B = ^2∆/_ca ; sin C = ^2∆/_ab

(xiii) r = ∆/s.

(xiv) r = 4R sin (A/2) sin (B/2) sin (C/2).

(xv) r = (s - a) tan (A/2) = (s - b) tan (B/2) = (s - c) tan (C/2).

(xvi) r₁ = ∆/(s - a) ; r₂ = ∆/(s - b); r₃ = ∆/(s - c) .

(xvii) r₁ = 4 R sin (A/2) cos (B/2) cos (C/2).

(xviii) r₂ = 4R sin (B/2) cos (C/2) cos (A/2).

(xix) r₃ = 4 R sin (C/2) cos (A/2) cos (B/2).

(xx) r₁ = s tan (A/2) ; r₂ = s tan (B/2) ; r₃ = s tan (C/2).

`

● Formula

• Basic Math Formulas
  
• Math Formula Sheet on Co-Ordinate Geometry
  
• All Math Formula on Mensuration
  
• Simple Math Formula on Trigonometry

11 and 12 Grade Math

From Simple Math Formula on Trigonometry to HOME PAGE