Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Facts about Addition
The operation to find the total of different values is called addition.
● When we sum up two or more amounts we use addition.
● The sign of addition is +
● Add numbers in any order, we get the same sum. e.g.
5 + 6 + 7 = 18
6 + 7 + 5 = 18
7 + 5 + 6 = 18
● Zero added to any number gives the same number. e.g.
8 + 0 = 8
0 + 10 = 10
32 + 0 = 32
0 + 88 = 88
● Add 1 to a number, we get the next number. e.g.
11 + 1 = 12
40 + 1 = 41
1 + 76 = 77
1 + 99 = 100
Add:
5 + 0 =
0 + 25 =
15 + 1 =
68 + 1 =
22 + 8 + 5 =
5 + 8 + 22 =
8 + 5 + 22 =
5 + 4 + 3 + 2 =
6 + 7 + 5 + 0 =
9 + 1 + 4 + 7 =
Expand and add:
(i)
|
37 30 + 7 30 + 20 50 |
+ + + + 59 |
22 20 + 2 7 + 2 9 |
(ii)
245 + 652
200 + 40 + 5 + 600 + 50 + 2
200 + 600 + 40 + 50 + 5 + 2
800 + 90 + 7
897
Let us know some facts about addition which will help us to learn to add 4-digit and 5-digit numbers.
1. Addition of small numbers can be done horizontally.
Example: 6 + 2 + 3 = 11
2. Large numbers are added in vertical columns (written under the place value chart).
Example:
Th H T O
7 2 5 8
1 3 6 2
+ 1 4 2 6
1 0 0 4 6
3. A zero added to a number does not change the place value of the number.
H T O
3 2 5
+ 0
3 2 5
4. The number or values being added are called addends and the answer is called the sum.
5. 1 added to a number gives the successor of the number as the sum.
6. To find a missing addend in an addition sum, the given addend or the sum of all the given addends is subtracted from the given sum.
Workings:
7. Changing the order of the addend in an addition sum does not change the answer.
Example: (i) 45 + 26 = 26 + 45 = 71
(ii) 3 + 2 + 6 = 6 + 2 + 3 = 11
8. While adding more than two numbers, we can group any two numbers first. It does not change the sum.
Example: 7 + (9 + 3) = 7 + 12 = 19
or
(7 + 3) + 9 = 10 + 9 = 19
This fact helps us to group any two addends to make addition easy.
Example:
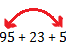
= (95 + 5) + 23
= 100 + 23
= 123
Let us have a quick review of what we have learnt about addition of 3- digit number in the previous class.
To add 2- digit numbers, the numbers are written one below the others. The tens and ones digits should appear are below the other.
Addition Facts:
You have two marbles. I give you one. How many will you have?
There are 3 marbles in all. Here the sign = stands for 'are equal to'. Now two marbles and one marble taken together make three marbles. That means if you add 1 to 2, you have 3.
If I give you two marbles and you have two marbles, how many will you have?
You have now four marbles. 2 and 2 added together make 4.
Now you have two marbles and I give you three. How many will you have?
You have 5 marbles. 2 and 3 added together make 5.
If you have three marbles and I give you three more, how many will you have?
You have now 6 marbles. 3 and 3 added together make 6.
If Tom has five marbles and you give him four more, he will have 9 marbles. Count them. 5 and 4 added together make 9.
Zero: If you have no marbles at all, you have zero marbles.
Zero is written like this 0 and means not any or nothing. If you add 5 to 0, it is still 5. If you add 0 to any number the sum is the same as the number itself.
Questions and Answers on 3rd Grade Addition Fact:
1. Solve the following sums and match them with the correct answer.
|
a. 20 + 5 b. 13 + 8 c. 17 + 7 d. 12 + 1 e. 14 + 6
f. 9 + 9 |
1. 20 2. 18 3. 21 4. 24 5. 13
6. 25 |
Answer:
1. a. → 6
b. → 3
c. → 4
d. → 5
e. → 1
f. → 2
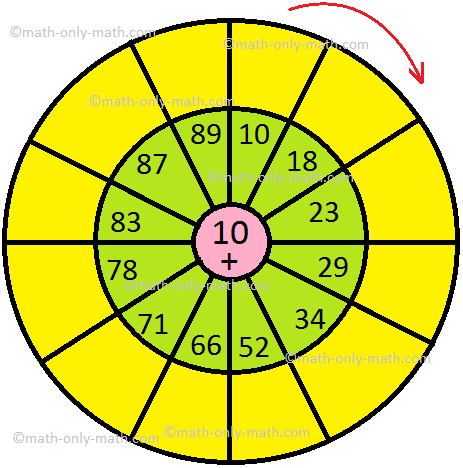
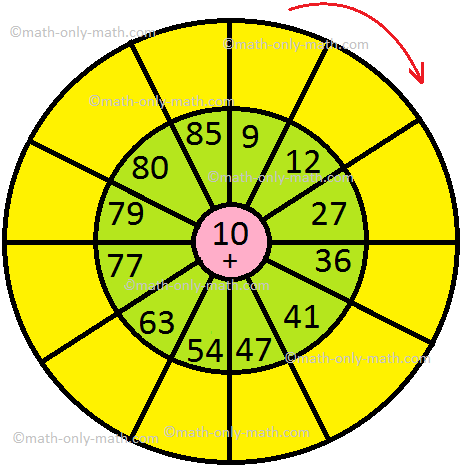
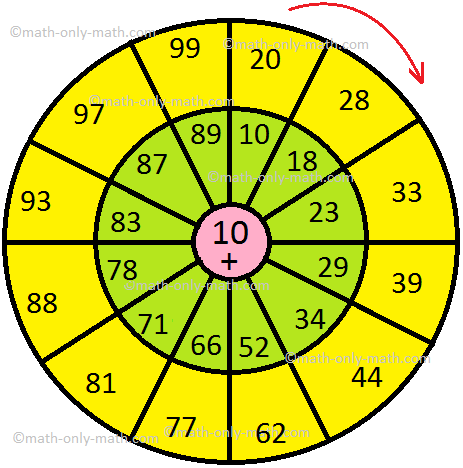
2. Add the number of the middle circle with the number given in the inner circle. Write the sum in the outer circle:
(i)
(ii)
Answer:
2. (i)
(ii)
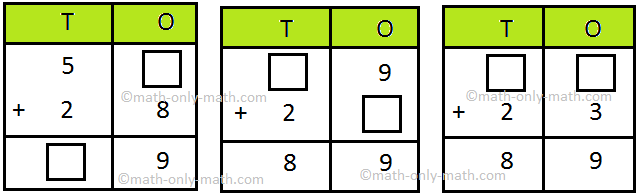
3. Fill in the missing numbers:
Answer:
3.
4. Add the following numbers:
(i) 34 + 3 = _____
(ii) 53 + 12 = _____
(iii) 17 + 8 = _____
(iv) 46 + 18 = _____
(v) 60 + 11 = _____
(vi) 82 + 6 = _____
(vii) 72 + 22 = _____
(viii) 21 + 5 = _____
Answer:
4. (i) 37
(ii) 65
(iii) 25
(iv) 64
(v) 671
(vi) 88
(vii) 94
(viii) 26
5. Write 'T' for True and 'F' for False Statement:
(i) The sum is always greater than the numbers being added.
(ii) When we change the order of number while adding the sum does change.
(iii) The sum of zero and any number is the number before it.
(iv) When you add 1 to a number the answer is the number after it.
Answer:
5. (i) T
(ii) F
(iii) F
(iv) T
From Facts about Addition to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.





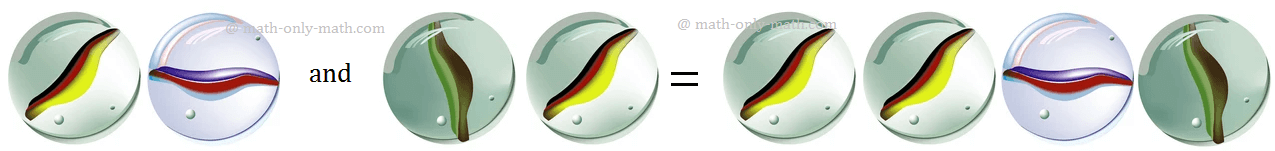




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.