Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Quadrilateral
What is quadrilateral?
A simple closed figure formed by joining four line segments is called a quadrilateral.
It has 4 sides, 4 angles, 4 vertices and two diagonals.
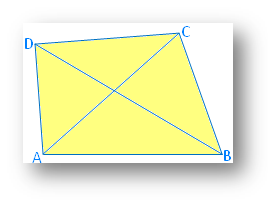
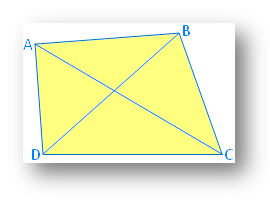
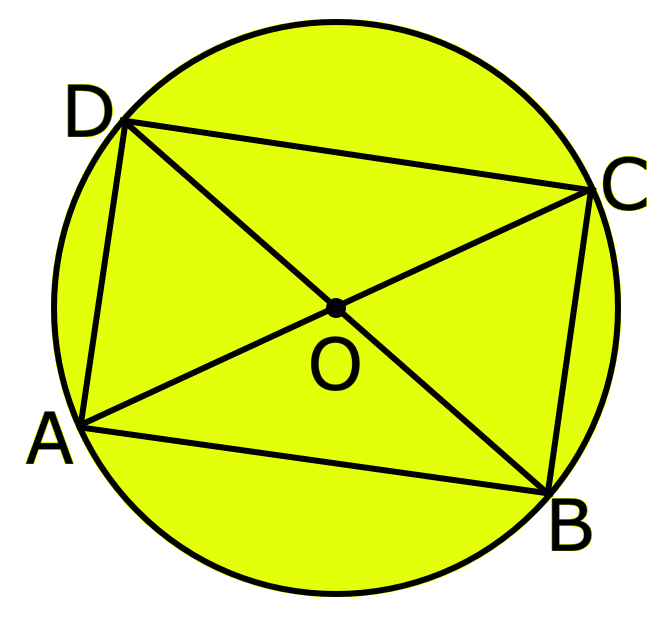
In a quadrilateral if A, B, C, D are four points in a plane such that no three of them are collinear and the line segments AB, BC, CD and DA do not intersect except at their end points.
Then, the figure formed by these four line segments is called the quadrilateral ABCD.
In a
quadrilateral ABCD ..
(i) the four points A, B, C, D are called its vertices,
(ii) the four line segments AB, BC, CD and DA are called its sides,
(iii) ∠DAB, ∠ABC, ∠BCD and ∠CDA are called its angles, to be denoted by ∠A, ∠B, ∠C and ∠D
respectively, and
(iv) the line segments AC and BD are called its diagonals.
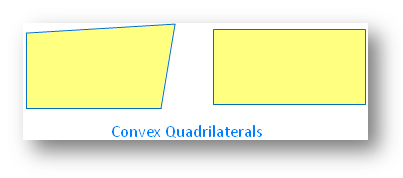
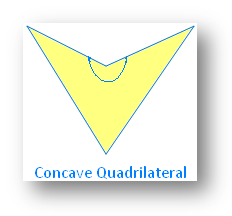
Convex Quadrilaterals and Concave Quadrilaterals:
If each angle of the quadrilateral is less than 180°, it is called a convex quadrilateral.
If at least one angle of the quadrilateral is more than 180°, it is called a concave quadrilateral.
Note:
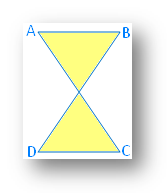
This figure is not a quadrilateral because it is not a simple closed figure.
Sides, Angles, Vertices, Diagonals of the Quadrilateral:
Adjacent Sides of a Quadrilateral
Two sides of
a quadrilateral which have a common end point are called its adjacent sides.
In the given figure, (AB, BC), (BC, CD), (CD, DA) and (DA, AB) are four pairs of adjacent sides of quadrilateral ABCD.
Opposite Sides of a Quadrilateral
Two sides of
a quadrilateral are called its opposite sides if they do not have a
common end point.
In the given figure, (AB, DC) and (AD, BC) are two pairs of opposite sides of quadrilateral ABCD.
Adjacent Angles of a Quadrilateral
Two angles
of a quadrilateral having a common arm are called its adjacent angles.
In the given figure, (∠A, ∠B), (∠B, ∠C), (∠C, ∠D) and (∠D, ∠A) are four pairs of adjacent angles of quadrilateral ABCD.
Opposite Angles of a Quadrilateral
Two angles
of a quadrilateral which are not adjacent angles are known as opposite
angles.
In the given figure, (∠A, ∠C) and (∠B, ∠D) are two pairs of opposite angles of quadrilateral ABCD.
Adjacent Vertices of a Quadrilateral:
Two vertices which have a common side are called adjacent vertices.
In the given figure, the pairs of adjacent vertices are (A, B); (B, C); (C, D) and (D, A).
Opposite Vertices of a Quadrilateral:
Two vertices which do not have a common side are called opposite vertices.
In the given figure, the pairs of opposite vertices are (A, C) and (B, D).
Diagonal of a Quadrilateral:
The line segment joining the opposite vertices of quadrilateral is the diagonal of the quadrilateral.
In the given figure, the two diagonals are AC and BD.
● Related Concepts on Quadrilateral
● Different Types of Quadrilaterals
● Construction of Quadrilaterals
● Construct Different Types of Quadrilaterals
● Quadrilateral - Worksheets
● Worksheet on Construction on Quadrilateral
● Worksheet on Different Types of Quadrilaterals
8th Grade Math Practice
From Quadrilateral to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 15, 25 02:46 AM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
5th Grade Quadrilaterals | Square | Rectangle | Parallelogram |Rhombus
Jul 15, 25 02:01 AM
Quadrilaterals are known as four sided polygon.What is a quadrilateral? A closed figure made of our line segments is called a quadrilateral. For example: -
Formation of Numbers | Smallest and Greatest Number| Number Formation
Jul 14, 25 01:53 AM
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9, -
5th Grade Geometry Practice Test | Angle | Triangle | Circle |Free Ans
Jul 14, 25 01:53 AM
In 5th grade geometry practice test you will get different types of practice questions on lines, types of angle, triangles, properties of triangles, classification of triangles, construction of triang… -
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
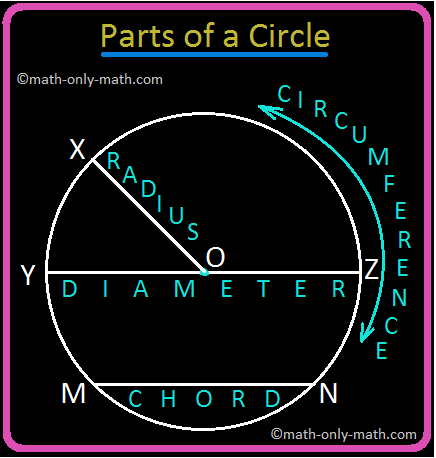
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.