Probability for Rolling Two Dice
Probability for rolling two dice with the six sided dots such as 1, 2, 3, 4, 5 and 6 dots in each die.
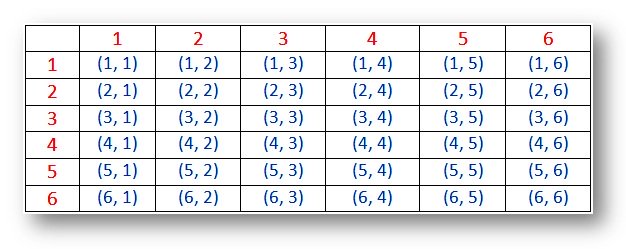
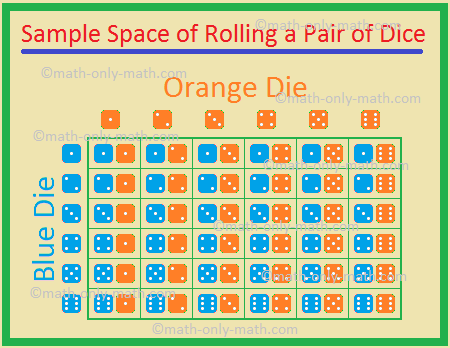
When two dice are thrown simultaneously, thus number of event can be 62 = 36 because each die has 1 to 6 number on its faces. Then the possible outcomes are shown in the below table.Probability – Sample space for two dice (outcomes):
Note:
(i) The outcomes (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6) are called doublets.
(ii) The pair (1, 2) and (2, 1) are different outcomes.
Worked-out problems involving probability for rolling two dice:
1. Two dice are rolled. Let A, B, C be the events of getting a sum of 2, a sum of 3 and a sum of 4 respectively. Then, show that
(i) A is a simple event
(ii) B and C are compound events
(iii) A and B are mutually exclusive
Solution:
Clearly, we have
A = {(1, 1)}, B = {(1, 2), (2, 1)} and C = {(1, 3), (3, 1), (2, 2)}.
(i) Since A consists of a single sample point, it is a simple event.
(ii) Since both B and C contain more than one sample point, each one of them is a compound event.
(iii) Since A ∩ B = ∅, A and B are mutually exclusive.
2. Two dice are rolled. A is the event that the sum of the numbers shown on the two dice is 5, and B is the event that at least one of the dice shows up a 3.
Are the two events (i) mutually exclusive, (ii) exhaustive? Give arguments in support of your answer.
Solution:
When two dice are rolled, we have n(S) = (6 × 6) = 36.
Now, A = {(1, 4), (2, 3), (4, 1), (3, 2)}, and
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
Hence, A and B are not mutually exclusive.
(ii) Also, A ∪ B ≠ S.
Therefore, A and B are not exhaustive events.
More examples related to the questions on the probabilities for throwing two dice.
3. Two dice are thrown simultaneously. Find the probability of:
(i) getting six as a product
(ii) getting sum ≤ 3
(iii) getting sum ≤ 10
(iv) getting a doublet
(v) getting a sum of 8
(vi) getting sum divisible by 5
(vii) getting sum of atleast 11
(viii) getting a multiple of 3 as the sum
(ix) getting a total of atleast 10
(x) getting an even number as the sum
(xi) getting a prime number as the sum
(xii) getting a doublet of even numbers
(xiii) getting a multiple of 2 on one die and a multiple of 3 on the other die
Solution:
Two different dice are thrown simultaneously being number 1, 2, 3, 4, 5 and 6 on their faces. We know that in a single thrown of two different dice, the total number of possible outcomes is (6 × 6) = 36.
(i) getting six as a product:
Let E1 = event of getting six as a product. The number whose product is six will be E1 = [(1, 6), (2, 3), (3, 2), (6, 1)] = 4Therefore, probability of getting ‘six as a product’
Number of favorable outcomesP(E1) = Total number of possible outcome
= 4/36
= 1/9
(ii) getting sum ≤ 3:
Let E2 = event of getting sum ≤ 3. The number whose sum ≤ 3 will be E2 = [(1, 1), (1, 2), (2, 1)] = 3Therefore, probability of getting ‘sum ≤ 3’
Number of favorable outcomesP(E2) = Total number of possible outcome
= 3/36
= 1/12
(iii) getting sum ≤ 10:
Let E3 = event of getting sum ≤ 10. The number whose sum ≤ 10 will be E3 =[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5),
(6, 1), (6, 2), (6, 3), (6, 4)] = 33
Therefore, probability of getting ‘sum ≤ 10’
Number of favorable outcomesP(E3) = Total number of possible outcome
= 33/36
= 11/12
(iv) getting a doublet: Let E4 = event of getting a doublet. The number which doublet will be E4 = [(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)] = 6
Therefore, probability of getting ‘a doublet’
Number of favorable outcomesP(E4) = Total number of possible outcome
= 6/36
= 1/6
(v) getting a sum of 8:
Let E5 = event of getting a sum of 8. The number which is a sum of 8 will be E5 = [(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)] = 5Therefore, probability of getting ‘a sum of 8’
Number of favorable outcomesP(E5) = Total number of possible outcome
= 5/36
(vi) getting sum divisible by 5:
Let E6 = event of getting sum divisible by 5. The number whose sum divisible by 5 will be E6 = [(1, 4), (2, 3), (3, 2), (4, 1), (4, 6), (5, 5), (6, 4)] = 7Therefore, probability of getting ‘sum divisible by 5’
Number of favorable outcomesP(E6) = Total number of possible outcome
= 7/36
(vii) getting sum of atleast 11:
Let E7 = event of getting sum of atleast 11. The events of the sum of atleast 11 will be E7 = [(5, 6), (6, 5), (6, 6)] = 3Therefore, probability of getting ‘sum of atleast 11’
Number of favorable outcomesP(E7) = Total number of possible outcome
= 3/36
= 1/12
(viii) getting a multiple of 3 as the sum:
Let E8 = event of getting a multiple of 3 as the sum. The events of a multiple of 3 as the sum will be E8 = [(1, 2), (1, 5), (2, 1), (2, 4), (3, 3), (3, 6), (4, 2), (4, 5), (5, 1), (5, 4), (6, 3) (6, 6)] = 12Therefore, probability of getting ‘a multiple of 3 as the sum’
Number of favorable outcomesP(E8) = Total number of possible outcome
= 12/36
= 1/3
(ix) getting a total of atleast 10:
Let E9 = event of getting a total of atleast 10. The events of a total of atleast 10 will be E9 = [(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)] = 6Therefore, probability of getting ‘a total of atleast 10’
Number of favorable outcomesP(E9) = Total number of possible outcome
= 6/36
= 1/6
(x) getting an even number as the sum:
Let E10 = event of getting an even number as the sum. The events of an even number as the sum will be E10 = [(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 3), (3, 1), (3, 5), (4, 4), (4, 2), (4, 6), (5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6)] = 18Therefore, probability of getting ‘an even number as the sum
Number of favorable outcomesP(E10) = Total number of possible outcome
= 18/36
= 1/2
(xi) getting a prime number as the sum:
Let E11 = event of getting a prime number as the sum. The events of a prime number as the sum will be E11 = [(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)] = 15Therefore, probability of getting ‘a prime number as the sum’
Number of favorable outcomesP(E11) = Total number of possible outcome
= 15/36
= 5/12
(xii) getting a doublet of even numbers:
Let E12 = event of getting a doublet of even numbers. The events of a doublet of even numbers will be E12 = [(2, 2), (4, 4), (6, 6)] = 3Therefore, probability of getting ‘a doublet of even numbers’
Number of favorable outcomesP(E12) = Total number of possible outcome
= 3/36
= 1/12
(xiii) getting a multiple of 2 on one die and a multiple of 3 on the other die:
Let E13 = event of getting a multiple of 2 on one die and a multiple of 3 on the other die. The events of a multiple of 2 on one die and a multiple of 3 on the other die will be E13 = [(2, 3), (2, 6), (3, 2), (3, 4), (3, 6), (4, 3), (4, 6), (6, 2), (6, 3), (6, 4), (6, 6)] = 11Therefore, probability of getting ‘a multiple of 2 on one die and a multiple of 3 on the other die’
Number of favorable outcomesP(E13) = Total number of possible outcome
= 11/36
4. Two dice are thrown. Find (i) the odds in favour of getting the sum 5, and (ii) the odds against getting the sum 6.
Solution:
We know that in a single thrown of two die, the total number of possible outcomes is (6 × 6) = 36.
Let S be the sample space. Then, n(S) = 36.
(i) the odds in favour of getting the sum 5:
Let E1 be the event of getting the sum 5. Then,E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
Therefore, P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ odds in favour of E1 = P(E1)/[1 – P(E1)] = (1/9)/(1 – 1/9) = 1/8.
(ii) the odds against getting the sum 6:
Let E2 be the event of getting the sum 6. Then,E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Therefore, P(E2) = n(E2)/n(S) = 5/36
⇒ odds against E2 = [1 – P(E2)]/P(E2) = (1 – 5/36)/(5/36) = 31/5.
5. Two dice, one blue and one orange, are rolled simultaneously. Find the probability of getting
(i) equal numbers on both
(ii) two numbers appearing on them whose sum is 9.
Solution:
The possible outcomes are
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
Therefore, total number of possible outcomes = 36.
(i) Number of favourable outcomes for the event E
= number of outcomes having equal numbers on both dice
= 6 [namely, (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)].
So, by definition, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Number of favourable outcomes for the event F
= Number of outcomes in which two numbers appearing on them have the sum 9
= 4 [namely, (3, 6), (4, 5), (5, 4), (3, 6)].
Thus, by definition, P(F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
These examples will help us to solve different types of problems based on probability for rolling two dice.
Probability
Probability of Tossing Two Coins
Probability of Tossing Three Coins
Probability for Rolling Two Dice
Probability for Rolling Three Dice
From Probability for Rolling Two Dice to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Adding 1-Digit Number | Understand the Concept one Digit Number
Apr 26, 24 01:55 PM
Understand the concept of adding 1-digit number with the help of objects as well as numbers. -
Subtracting 2-Digit Numbers | How to Subtract Two Digit Numbers?
Apr 26, 24 12:36 PM
In subtracting 2-digit numbers we will subtract or minus a two-digit number from another two-digit number. To find the difference between the two numbers we need to ‘ones from ones’ and ‘tens from -
1st Grade Word Problems on Subtraction | Subtracting 2-Digit Numbers
Apr 26, 24 12:06 PM
In 1st grade word problems on subtraction students can practice the questions on word problems based on subtraction. This exercise sheet on subtraction can be practiced by the students to get more ide… -
Subtracting 1-Digit Number | Subtract or Minus Two One-Digit Number
Apr 26, 24 11:21 AM
In subtracting 1-digit number we will subtract or minus one-digit number from one-digit number or one-digit number from 2-digit number and find the difference between them. We know that subtraction me… -
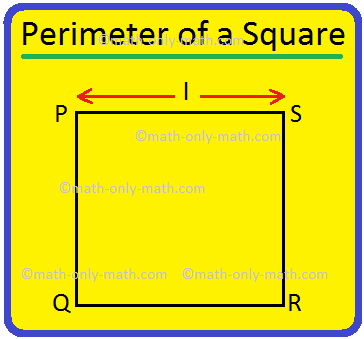
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete…