Power of Literal Quantities
Power of literal quantities means when a quantity is multiplied by itself, any number of times, the product is called a power of that quantity. This product is expressed by writing the number of factors in it to the right of the quantity and slightly raised.
For example:
(i) m × m has two factors so to express it we can write m × m = m2(ii) b × b × b has three factors so to express it we can write b × b × b = b3
(iii) z × z × z × z × z × z × z has seven factors so to express it we can write z × z × z × z × z × z × z = z7
Learn how to read and write the power of literal quantities.
(i) Product of x × x is written as x2 and it is read as x squared or x raised to the power 2.(ii) Product of y × y × y is written as y3 and it is read as y cubed or y raised to the power 3.
(iii) Product of n × n × n × n is written as n4 and it is read as forth power of n or n raised to the power 4.
(iv) Product of 3 × 3 × 3 × 3 × 3 is written as 35 and it is read as fifth power of 3 or 3 raised to the power 5.
How to identify the base and exponent of the power of the given quantity?
(i) In a5 here a is called the base and 5 is called the exponent or index or power.(ii) In Mn here M is called the base and n is called the exponent or index or power.
Solved examples:
1. Write a × a × b × b × b in index form.
a × a × b × b × b = a2b32. Express 5 × m × m × m × n × n in power form.
5 × m × m × m × n × n = 5m3n2
3. Express -5 × 3 × p × q × q × r in exponent form.
-5 × 3 × p × q × q × r = -15pq2r
4. Write 3x3y4 in product form.
3x3y4 = 3 × x × x × x × y × y × y × y
5. Express 9a4b2c3 in product form.
9a4b2c3 = 3 × 3 × a × a × a × a × b × b × c × c × c
● Terms of an Algebraic Expression
Types of Algebraic Expressions
Multiplication of Two Monomials
Multiplication of Polynomial by Monomial
Multiplication of two Binomials
Algebra Page
6th Grade Page
From Power of Literal Quantities to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
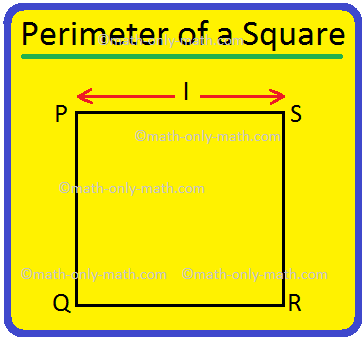
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
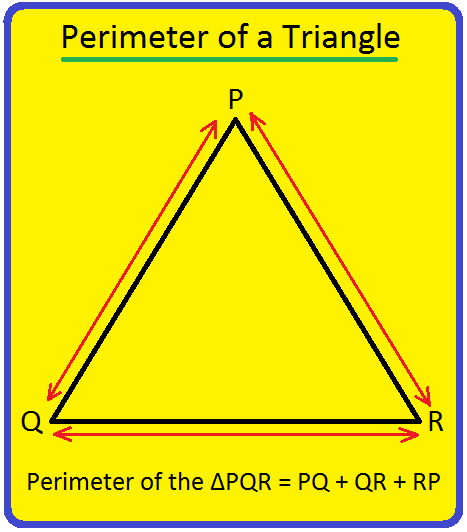
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
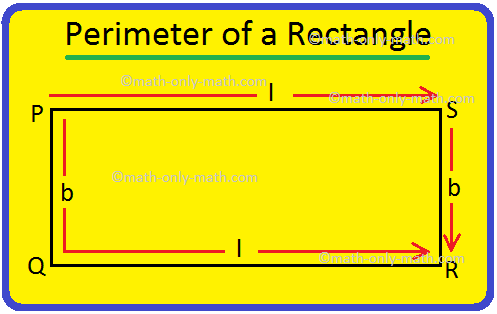
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…
● Terms of an Algebraic Expression - Worksheet
Worksheet on Types of Algebraic Expressions
Worksheet on Degree of a Polynomial
Worksheet on Addition of Polynomials
Worksheet on Subtraction of Polynomials
Worksheet on Addition and Subtraction of Polynomials
Worksheet on Adding and Subtracting Polynomials
Worksheet on Multiplying Monomials
Worksheet on Multiplying Monomial and Binomial
Worksheet on Multiplying Monomial and Polynomial