Learn math step-by-step.
Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Math Formula Sheet on Co-Ordinate Geometry
All grade math formula sheet on co-ordinate geometry. These math formula charts can be used by 10th grade, 11th grade, 12th grade and college grade students to solve co-ordinate geometry.
Co-Ordinate Geometry
● Rectangular Cartesian Co-ordinates:
(i) If the pole and initial line of the polar system coincides respectively with the origin and positive x-axis of the Cartesian system and (x, y), (r, θ) be the Cartesian and polar co-ordinates respectively of a point P on the plane then,x = r cos θ, y = r sin θ
and r = √(x2 + y2), θ = tan-1(y/x).
(ii) The distance between two given points P (x1, y1) and Q (x2, y2) is
PQ = √{(x2 - x1)2 + (y2 - y1)2}.
(iii) Let P (x1, y1) and Q (x2, y2) be two given points.
(a) If the point R divides the line-segment PQ internally in the ratio m : n, then the co-ordinates of R
are {(mx2 + nx1)/(m + n) , (my2 + ny1)/(m + n)}.
(b) If the point R divides the line-segment PQ externally in the ratio m : n, then the co-ordinates of R are
{(mx2 - nx1)/(m - n), (my2 - ny1)/(m - n)}.
(c) If R is the mid-point of the line-segment PQ, then the co-ordinates of R are {(x1 + x2)/2, (y1 + y2)/2}.
(iv) The co-ordinates of the centroid of the triangle formed by joining the points (x1, y1) , (x2, y2) and (x3, y3) are
({x1 + x2 + x3}/3 , {y1 + y2 + y3}/3
(v) The area of a triangle formed by joining the points (x1, y1), (x2, y2) and (x3, y3) is
½ | y1 (x2 - x3) + y2 (x3 - x1) + y3 (x1 - x2) | sq. units
or, ½ | x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2) | sq. units.
● Straight Line:
(i) The slope or gradient of a straight line is the trigonometric tangent of the angle θ which the line makes with the positive directive of x-axis.(ii) The slope of x-axis or of a line parallel to x-axis is zero.
(iii) The slope of y-axis or of a line parallel to y-axis is undefined.
(iv) The slope of the line joining the points (x1, y1) and (x2, y2) is
m = (y2 - y1)/(x2 - x1).
(v) The equation of x-axis is y = 0 and the equation of a line parallel to x-axis is y = b.
(vi) The equation of y-axis is x = 0 and the equation of a line parallel to y-axis is x = a.
(vii) The equation of a straight line in
(a) slope-intercept form: y = mx + c where m is the slope of the line and c is its y-intercept;
(b) point-slope form: y - y1 = m (x - x1) where m is the slope of the line and (x1 , y1) is a given point on the line;
(c) symmetrical form: (x - x1)/cos θ = (y - y1)/sin θ = r, where θ is the inclination of the line, (x1, y1) is a given point on the line and r is the distance between the points (x, y) and (x1, y1);
(d) two-point form: (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) where (x1, y1) and (x2, y2) are two given points on the line;
(e) intercept form: x/a + y/b = 1 where a = x-intercept and b = y-intercept of the line;
(f) normal form: x cos α + y sin α = p where p is the perpendicular distance of the line from the origin and α is the angle which the perpendicular line makes with the positive direction of the x-axis.
(g) general form: ax + by + c = 0 where a, b, c are constants and a, b are not both zero.
(viii) The equation of any straight line through the intersection of the lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 is a1x + b1y + c + k(a2x + b2y + c2) = 0 (k ≠ 0).
(ix) If p ≠ 0, q ≠ 0, r ≠ 0 are constants then the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 and a3x + b3y + c3 = 0 are concurrent if P(a1x + b1y + c1) + q( a2x + b2y + c2) + r(a3x + b3y + c3) = 0.
(x) If θ be the angle between the lines y= m1x + c1 and y = m2x + c2 then tan θ = ± (m1 - m2 )/(1 + m1 m2);
(xi) The lines y= m1x + c1 and y = m2x + c2 are
(a) parallel to each other when m1 = m2;
(b) perpendicular to one another when m1 ∙ m2 = - 1.
(xii) The equation of any straight line which is
(a) parallel to the line ax + by + c = 0 is ax + by = k where k is an arbitrary constant;
(b) perpendicular to the line ax + by + c = 0 is bx - ay = k1 where k1 is an arbitrary constant.
(xiii) The straight lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are identical if a1/a2 = b1/b2 = c1/c2.
(xiv) The points (x1, y1) and (x2, y2) lie on the same or opposite sides of the line ax + by + c = 0 according as (ax1 + by1 + c) and (ax2 + by2 + c) are of same sign or opposite signs.
(xv) Length of the perpendicular from the point (x1, y1) upon the line ax + by + c = 0 is|(ax1 + by1 + c)|/√(a2 + b2).
(xvi) The equations of the bisectors of the angles between the lines a1x + b1y + c1 = 0 and a2x + b2y + c2 =0 are
(a1x + b1y + c1)/√(a12 + b12) = ± (a2x + b2y + c2)/√(a22 + b22).
● Circle:
(i) The equation of the circle having centre at the origin and radius a units is x2 + y2 = a2 . . . (1)The parametric equation of the circle (1) is x = a cos θ, y = a sin θ, θ being the parameter.
(ii) The equation of the circle having centre at (α, β) and radius a units is (x - α)2 + (y - β)2 = a2.
(iii) The equation of the circle in general form is x2 + y2 + 2gx + 2fy + c = 0 The centre of this circle is at (-g, -f) and radius = √(g2 + f2 - c)
(iv) The equation ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a circle if a = b (≠ 0) and h = 0.
(v) The equation of a circle concentric with the circle x2 + y2 + 2gx + 2fy + c = 0 is x2 + y2 + 2gx + 2fy + k = 0 where k is an arbitrary constant.
(vi) If C1 = x2 + y2 + 2g1x + 2f1y + c1 = 0
and C2 = x2 + y2 + 2g2x + 2f2y + c2 = 0 then
(a) the equation of the circle passing through the points of intersection of C1 and C2 is C1 + kC2 = 0 (k ≠ 1);
(b) the equation of the common chord of C1 and C2 is C1 - C2 = 0.
(vii) The equation of the circle with the given points (x1, y1) and (x2, y2) as the ends of a diameter is (x - x1) (x - x2) + (y - y1) (y - y2) = 0.
(viii) The point (x1, y1) lies outside, on or inside the circle x2 + y2 + 2gx + 2fy + c = 0 according as x12 + y12 + 2gx1 + 2fy1 + c > , = or < 0.
● Parabola:
(i) Standard equation of parabola is y2 = 4ax. Its vertex is the origin and axis is x-axis.(ii) Other forms of the equations of parabola:
(a) x2 = 4ay.
Its vertex is the origin and axis is y-axis.
(b) (y - β)2 = 4a (x - α).
Its vertex is at (α, β) and axis is parallel to x-axis.
(c) (x - α)2 = 4a(y- β).
Its vertex is at ( a, β) and axis is parallel to y-axis.
(iii) x = ay2 + by + c (a ≠ o) represents equation of the parabola whose axis is parallel to x-axis.
(iv) y = px2 + qx + r (p ≠ o) represents equation of the parabola whose axis is parallel to y-axis.
(v) The parametric equations of the parabola y2 = 4ax are x = at2 , y = 2at, t being the parameter.
(vi) The point (x1, y1) lies outside, on or inside the parabola y2 = 4ax according as y12 = 4ax1 >, = or,<0
● Ellipse:
(i) Standard equation of ellipse isx2/a2 + y2/b2 = 1 ……….(1)
(a) Its centre is the origin and major and minor axes are along x and y-axes respectively ; length of major axis = 2a and that of minor axis = 2b and eccentricity = e = √[1 – (b2/a2)]
(b) If S and S’ be the two foci and P (x, y) any point on it then SP = a - ex, S’P = a + ex and SP + S’P = 2a.
(c) The point (x1, y1) lies outside, on or inside the ellipse (1) according as x12/a2 + y12/b2 - 1 > , = or < 0.
(d) The parametric equations of the ellipse (1) are x = a cos θ, y = b sin θ where θ is the eccentric angle of the point P (x, y) on the ellipse (1) ; (a cos θ, b sin θ) are called the parametric co-ordinates of P.
(e) The equation of auxiliary circle of the ellipse (1) is x2 + y2 = a2.
(ii) Other forms of the equations of ellipse:
(a) x2/a2 + y2/b2 = 1. Its centre is at the origin and the major and minor axes are along y and x-axes respectively.
(b) [(x - α)2]/a2 + [(y - β)2]/b2 = 1.
The centre of this ellipse is at (α, β) and the major and minor ones are parallel to x-axis and y-axis respectively.
● Hyperbola:
(i) Standard equation of hyperbola is x2/a2 - y2/b2 = 1 . . . (1)(a) Its centre is the origin and transverse and conjugate axes are along x and y-axes respectively ; its length of transverse axis = 2a and that of conjugate axis = 2b and eccentricity = e = √[1 + (b2/a2)].
(b) If S and S’ be the two foci and P (x, y) any point on it then SP = ex - a, S’P = ex + a and S’P - SP = 2a.
(c) The point (x1, y1) lies outside, on or inside the hyperbola (1) according as x12/a2 - y12/b2 = -1 < , = or, > 0.
(d) The parametric equation of the hyperbola (1 ) are x = a sec θ, y = b tan θ and the parametric co-ordinates of any point P on (1) are (a sec θ,b tan θ).
(e) The equation of auxiliary circle of the hyperbola (1) is x2 + y2 = a2.
(ii) Other forms of the equations of hyperbola:
(a) y2/a2 - x2/b2 = 1.
Its centre is the origin and transverse and conjugate axes are along y and x-axes respectively.
(b) [(x - α)2]/a2 - [(y - β)2]/b2 = 1. Its centre is at (α, β) and transverse and conjugate axes are parallel to x-axis and y-axis respectively.
(iii) Two hyperbolas
x2/a2 - y2/b2 = 1 ………..(2) and y2/b2 - x2/a2 = 1 …….. (3)
are conjugate to one another. If e1 and e2 be the eccentricities of the hyperbolas (2) and (3) respectively, then
b2 = a2 (e12 - 1) and a2 = b2 (e22 - 1).
(iv) The equation of rectangular hyperbola is x2 - y2 = a2 ; its eccentricity = √2.
● Intersection of a Straight Line with a Conic:
(i) The equation of the chord of the(a) circle x2 + y2 = a2 which is bisected at (x1, y1) is T = S1 where
T= xx1 + yy1 - a2 and S1 = x12 - y12 - a2 ;
(b) circle x2 + y2 + 2gx + 2fy + c = 0 which is bisected at (x1, y1) is T = S1 where T= xx1 + yy1 + g(x + x1) + f(y + y1) + c and S1 = x12 - y12 + 2gx1 +2fy1 + c;
(c) parabola y2 = 4ax which is bisected at (x1,y1) is T = S1 where T = yy1 - 2a (x + x1) and S1 = y12 - 4ax1;
(d) ellipse x2/a2 + y2/b2 = 1 which is bisected at (x1,y1) is T = S1
where T = (xx1)/a2 + (yy1)/b2 - 1 and S1 = x12/a2 + y12/b2 - 1.
(e) hyperbola x2/a2 - y2/b2 = 1 which is bisected at (x1, y1) is T = S1
where T = {(xx1)/a2} – {(yy1)/b2} - 1 and S1 = (x12/a2) + (y12/b2) - 1.
(ii) The equation of the diameter of a conic which bisects all chords parallel to the line y = mx + c is
(a) x + my = 0 when the conic is the circle x2 + y2 = a2 ;
(b) y = 2a/m when the conic is the parabola y2 = 4ax;
(c) y = - [b2/(a2m)] ∙ x when the conic is the ellipse x2/a2 + y2/b2 = 1
(d) y = [b2/(a2m )] ∙ x when the conic is the hyperbola x2/a2 - y2/b2 = 1
(iii) y = mx and y = m’x are two conjugate diameters of the
(a) ellipse x2/a2 + y2/b2 = 1 when mm’ = - b2/a2
(b) hyperbola x2/a2 - y2/b2 = 1 when mm’ = b2/a2.
● Formula
- Basic Math Formulas
- Math Formula Sheet on Co-Ordinate Geometry
- All Math Formula on Mensuration
- Simple Math Formula on Trigonometry
11 and 12 Grade Math
From Math Formula Sheet on Co-Ordinate Geometry to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
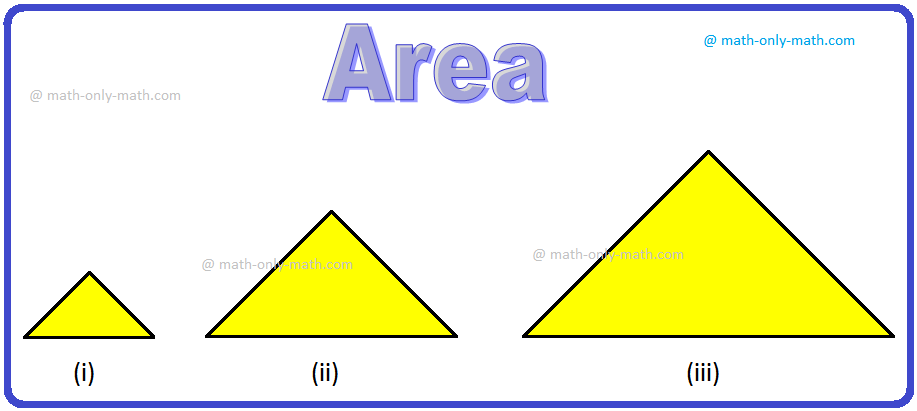
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
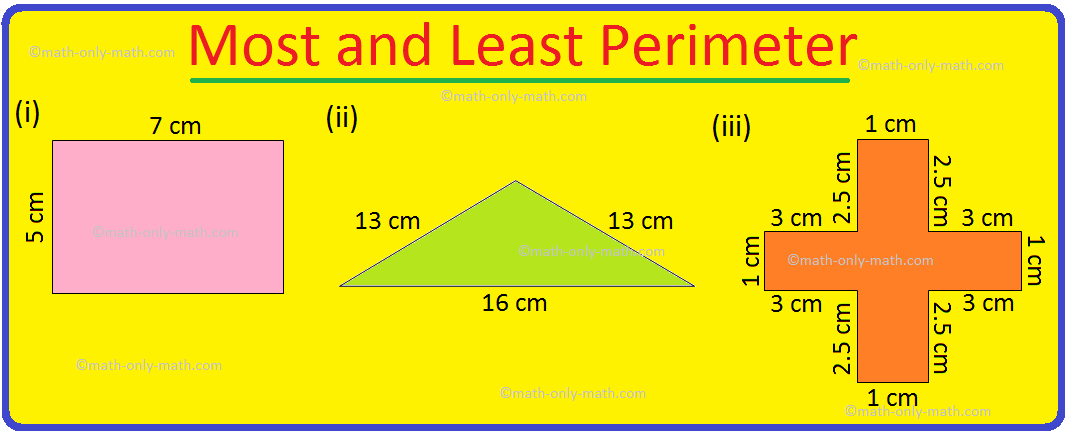
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
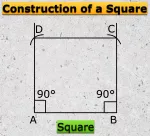
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
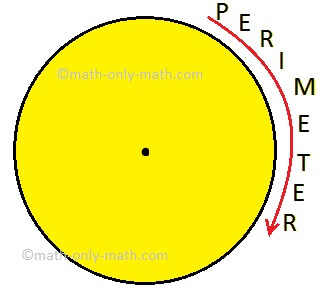
Perimeter of a Figure | Perimeter of a Simple Closed Figure | Examples
Jul 16, 25 02:33 AM
Perimeter of a figure is explained here. Perimeter is the total length of the boundary of a closed figure. The perimeter of a simple closed figure is the sum of the measures of line-segments which hav… -
Formation of Numbers | Smallest and Greatest Number| Number Formation
Jul 15, 25 11:46 AM
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.