Lines of Symmetry

Learn about lines of symmetry in different geometrical shapes.

It is not necessary that all the figures possess a line or lines of symmetry in different figures.

Figures may have:

No line of symmetry

1, 2, 3, 4 …… lines of symmetry

Infinite lines of symmetry

I: Symmetry of Geometrical Figures:

We know that a polygon is a closed figure with three or more line segments. A polygon is called regular if all of its sides and angles are equal. Thus, an equilateral triangle is a regular polygon of three sides. Similarly, regular polygon of four sides is called a square. The regular polygons are symmetrical figures and they have as as many lines of symmetry as they have sides or vertices.

Let us consider a list of examples and find out lines of symmetry in different figures:

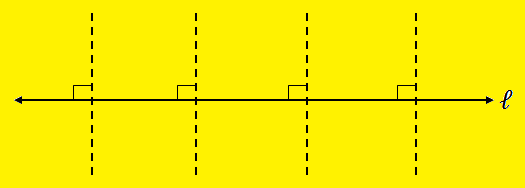
1. Symmetry of a Line:

A line has indefinite length and it can be considered that each line perpendicular to the given line divides the line into two equal halves. So a line has infinite symmetrical lines which are perpendicular to it. Also a line is symmetrical to itself.

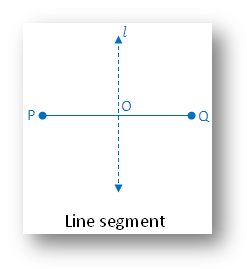
2. Symmetry of a Line Segment:

A line segment has two lines of symmetry, the segment itself and the perpendicular bisector of the segment.

The above figure is symmetric along the perpendicular bisector ℓ.

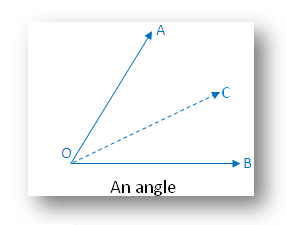
3. Symmetry of An angle:

An angle with equal arms has one line of symmetry-along the internal bisector of the angle.

In the figure there is one line of symmetry. The figure is symmetric along the angle bisector OC.

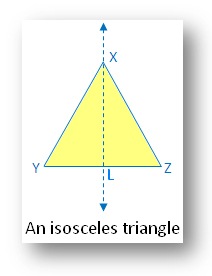
4. An isosceles triangle:

In the figure there is one line of symmetry. The figure is symmetric along the bisector of the vertical angle. The median XL.

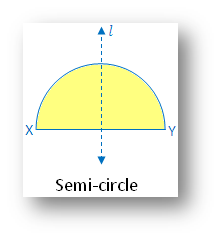
5. Semi-circle:

In the figure there is one line of symmetry. The figure is symmetric along the perpendicular bisector l. of the diameter XY.

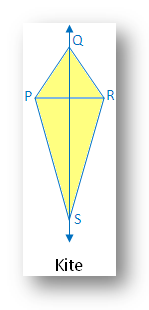
6. Symmetry of Kite:

A kite has one line of symmetry.

In the figure there is one line of symmetry. The figure is symmetric along the diagonal QS.

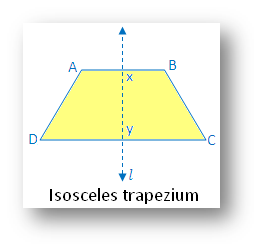
7. Isosceles trapezium:

In the figure there is one line of symmetry. The figure is symmetric along the line l joining the midpoints of two parallel sides AB and DC.

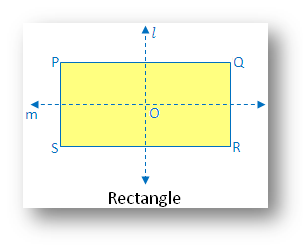
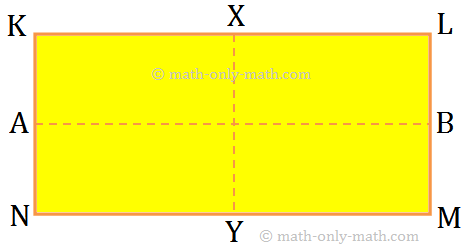
8. Rectangle:

In the figure there are two lines of symmetry. The figure is symmetric along the lines l and m joining the midpoints of opposite sides.

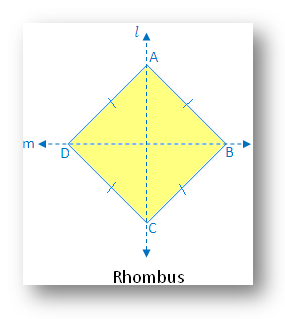
9. Rhombus:

A rhombus has two lines of symmetry-along the diagonals of the rhombus.

In the figure there are two lines of symmetry. The figure is symmetric along the diagonals AC and BD of the figure.

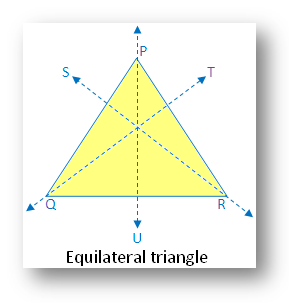
10. Equilateral Triangle:

An equilateral triangle has three lines of symmetry along the three medians.

In the above equilateral triangle there are three lines of symmetry. The figure is symmetric along the 3 medians PU, QT and RS.

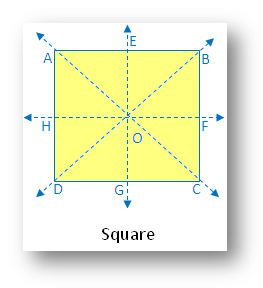
11. Square:

A square has four lines of symmetry - two along the line segments joining the mid-points of opposite sides and two along the diagonals.

In the figure there are four lines of symmetry. The figure is symmetric along the 2 diagonals and 2 midpoints of opposite sides.

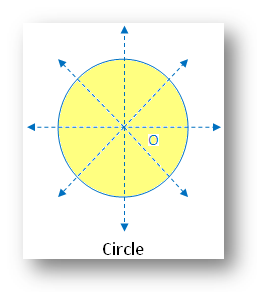
12. Symmetry of a Circle:

A circle has infinite number of lines of symmetry all along its diameters.

In the figure there are infinite lines of symmetry. The figure is symmetric along all the diameters.

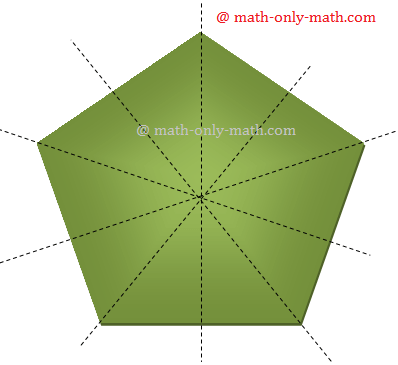
13. Regular Pentagon:

A regular pentagon has lines of symmetry as shown in the figure.

Other geometrical figures (polygon that are not regular) also have lines of symmetry but not as many as the number of sides.

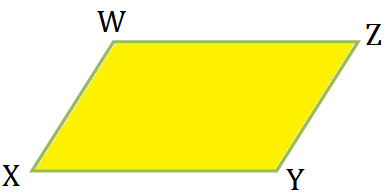
14. Symmetry of a Parallelogram:

A parallelogram has no line of symmetry. In the figure parallelogram WXYZ has no line of symmetry.

Note:

Each regular polygon (equilateral triangle, square, rhombus, regular pentagon, regular hexagon etc.) are symmetry.

The number of lines of symmetry in a regular polygon is equal to the number of sides a regular polygon has.

Some figures like scalene triangle and parallelogram have no lines of symmetry.

II: Symmetry in Letters of English Alphabet:

Lines of symmetry in letters of the English alphabet:

Letters having one line of symmetry:

A B C D E K M T U V W Y have one line of symmetry.

A M T U V W Y have vertical line of symmetry.

B C D E K have horizontal line of symmetry.

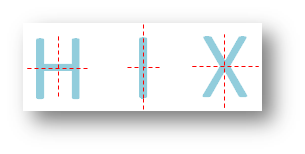
Letter having both horizontal and vertical lines of symmetry:

H I X have two lines of symmetry.

Letter having no lines of symmetry:

F G J L N P Q R S Z have neither horizontal nor vertical lines of symmetry.

Letters having infinite lines of symmetry:

O has infinite lines of symmetry. Infinite number of lines passes through the point symmetry about the center O with all possible diameters.

III: Examples on Lines of Symmetry:

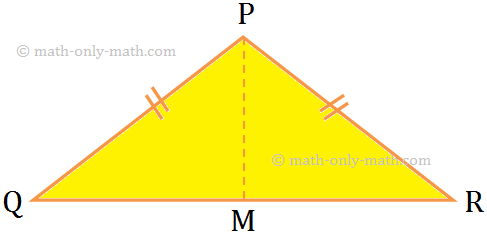
1. An isosceles triangle has one line of symmetry along the median through the vertex between equal sides. 

Median PM is a line of symmetry of isosceles triangle PQR as PQ = PR in the above figure.

2. A rectangle has two lines of symmetry-along the line segments joining the mid-points of the opposite sides.

In the above figure: AB and XY are two lines of symmetry of rectangle KLMN.

● Related Concepts

● Linear Symmetry

● Point Symmetry

● Rotational Symmetry

● Order of Rotational Symmetry

● Types of Symmetry

● Reflection

● Reflection of a Point in x-axis

● Reflection of a Point in y-axis

● Reflection of a point in origin

● Rotation

● 90 Degree Clockwise Rotation

● 90 Degree Anticlockwise Rotation

● 180 Degree Rotation

7th Grade Math Problems

8th Grade Math Practice

From Lines of Symmetry to HOME PAGE