Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Comparison between Two Rational Numbers
As we know that rational numbers are numbers which are represented in the form of pq where ‘p’ and ‘q’ are the integers with both negative and positive signs and ‘q’ is not equal to zero. In this topic of rational number we’ll compare the two rational numbers. Comparison is done between two numbers so as to find the greatest of two numbers. Comparison in this case will be somewhat similar to that of comparison we used to do between two whole numbers. But, there will be some differences from whole numbers’ case depending upon the type of rational numbers we are comparing.
We are aware that rational numbers are fractions. So, they can be classified into following types:
I. Proper rational number (fraction): Proper rational numbers are those which are less than 1. In this type of rational number denominator is greater than numerator, i.e., ‘p’ is less than ‘q’ in pq form.
For example: 23, 45, 79, etc. are all examples of proper fractions.
II. Improper rational numbers (fraction): Improper rational numbers are those which are greater than 1. In such type of rational numbers numerator is greater than denominator, i.e., ‘p’ is greater than q’ in pq form.
For example: 43, 98, 3412, etc. are all examples of improper rational numbers.
III. Positive rational number: In this type of rational number, both of the numerator and denominator are either positive or both of them are negative. These are always greater than zero.
For example: 23, −4−5, etc. are all examples of positive rational numbers.
IV. Negative rational number: In this type of rational number, either numerator is negative or denominator is negative. These are always less than zero.
For example: −25, 3−8, etc. are all examples of negative rational numbers.
Comparison between the numbers:
1. Before going to the comparison of rational numbers always remember following points:
(i) Every positive number is greater than zero.
(ii) Every negative number is less than zero.
(iii) Every positive number is greater than negative number.
(iv) Every number on the right of number line is greater than number on its left on the number line.
2. For comparison between two rational numbers we need to follow the below mentioned steps:
Step I: Firstly make sure that the denominators of the given rational numbers are positive. If not so multiply both numerator and denominator of the rational number by -1 to convert the negative denominator into positive. This will result into negative numerator and positive denominator.
Step II: Secondly, check for the rational numbers for like rational numbers (which have same denominator) and unlike rational numbers (which have different denominators).
Step III: If the rational numbers are like fractions, then we just need to compare the numerators and the one having higher denominator will be greater of the two. Don’t forget to check for negative and positive rational numbers.
Step IV: If the rational numbers are unlike fractions then convert them into like fractions by taking L.C.M. of the denominators and then compare them as given in step 1.
In short:
Let ab and cd be two rational numbers.
If one is positive and the other is negative, the positive number is greater than the negative number.
If both are positive (or negative), change both the numbers into fractions with common (positive) denominator. Next, compare the numerators. The fraction having the greater numerator is larger.
Solved examples on Comparison between Two Rational Numbers
1. Compare 2 and -4.
Solution:
We know that every positive number is greater than every negative number. Hence, 2 is greater than -4, i.e., 2 > (-4).
2. Compare 13 and 53.
Solution:
The given problem is of like fraction where denominators of the rational fraction are same and we just need to compare the numerators and the one having greater numerator will be the largest of the two. In this case 5 is greater than 1 and denominators of both are same, hence 13 is less than 53, i.e., 13 < 53.
3. Compare 13 and 56.
Solution:
The given problem is of unlike fraction where denominator of the rational fractions are different and for comparing them we need to take L.C.M. of the denominators and solve as shown below:
The L.C.M. of the denominators is 6.
Now, numbers will become
1×26 and 56, i.e., numbers will be 26 and 56. Now the example becomes of the like fraction type and since their denominators have become same, we only need to compare the numerators. Since, 2 is less than 5, so 26 will be less than 56. Hence, 13 is less than 56, i.e., 13 < 56.
4. Compare −23 and 9−4
Solution:
Since, the denominator 9−4is negative, we need to make it positive by multiplying both numerator and denominator by (-1). After multiplication we get −94.
Now, we have to make comparison between −23 and
−94. Now the example becomes of type comparison between unlike rational fractions.
Now, L.C.M. of the denominators is equal to 12.
Further the problem is solved by comparing the following two:
(−2)×412 and (−9)×312
Now the comparison is of like rational fractions.
−812and −2712
Since, denominator is same we only need to compare only denominators. The one having more numerator will be greater of the two rational fractions. Since, both of the numerators are negative in nature so the one to the right in number line will be more than the left one. Since, (-8) is at the right side and (-27) is on the left one. Hence, (-8) is greater than (-27). So, −812 is greater than −2712.
Hence, −23 is greater than 9−4.
Rational Numbers
Decimal Representation of Rational Numbers
Rational Numbers in Terminating and Non-Terminating Decimals
Recurring Decimals as Rational Numbers
Laws of Algebra for Rational Numbers
Comparison between Two Rational Numbers
Rational Numbers Between Two Unequal Rational Numbers
Representation of Rational Numbers on Number Line
Problems on Rational numbers as Decimal Numbers
Problems Based On Recurring Decimals as Rational Numbers
Problems on Comparison Between Rational Numbers
Problems on Representation of Rational Numbers on Number Line
Worksheet on Comparison between Rational Numbers
Worksheet on Representation of Rational Numbers on the Number Line
From Comparison between Two Rational Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
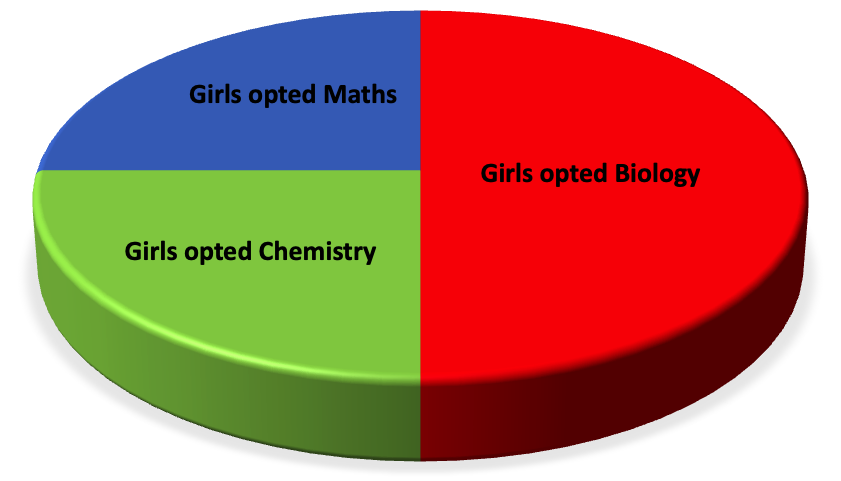
5th Grade Pie Chart | Definition of Pie Chart | Construction |Examples
Jul 31, 25 05:12 PM
Data can also be represented in a circle. This method, to represent data, is called a pie chart. Let us understand this method with the help of an example. -
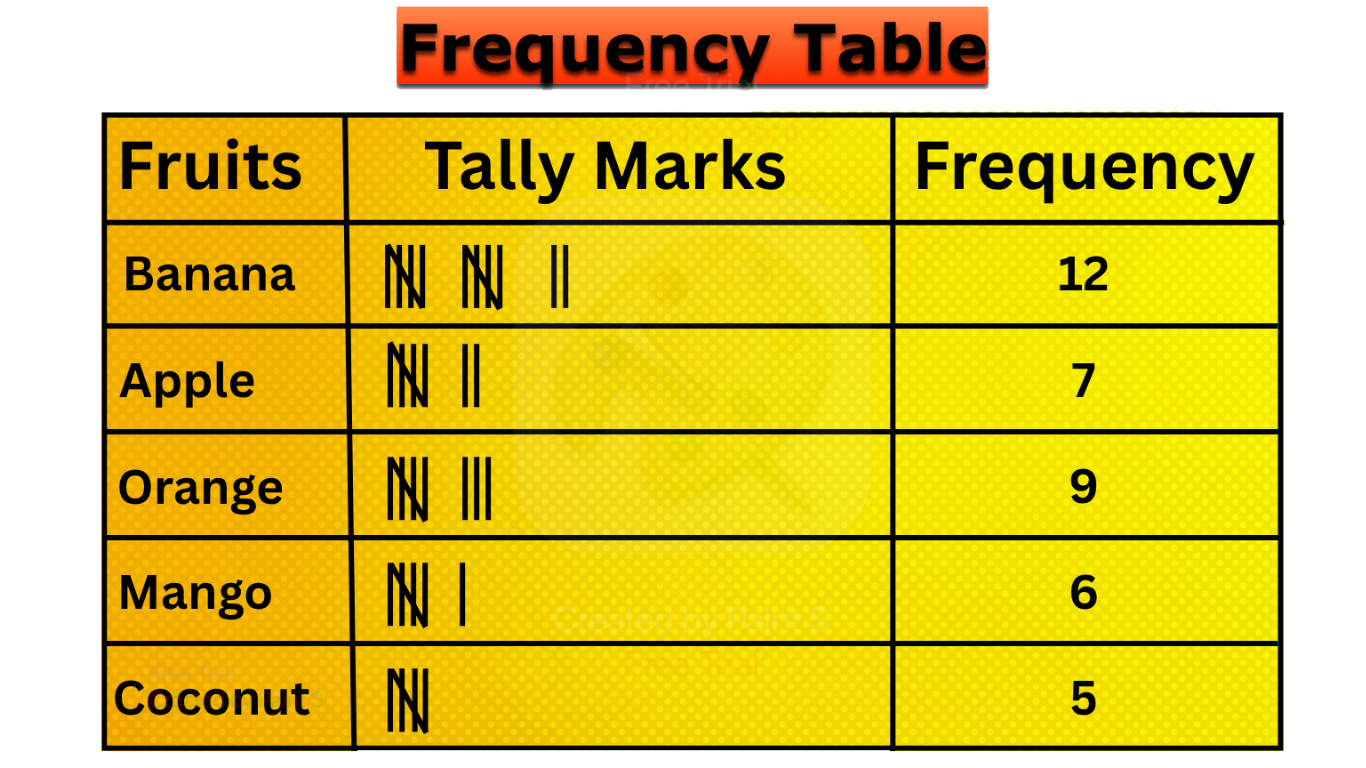
Frequency Distribution |Tally Marks |Frequency Distribution Table
Jul 31, 25 12:23 PM
What is frequency distribution?The number of times a particular observation occurs in a given data is called its frequency. In 7ᵗʰ grade and 8ᵗʰ grade frequency distribution, -
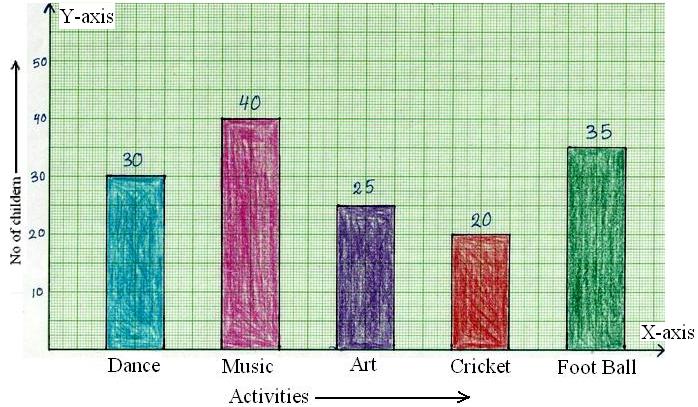
5th Grade Bar Graph | Definition | Interpret Bar Graphs|Free Worksheet
Jul 31, 25 05:16 AM
We learn how to represent the data on the bar graph. Data can be represented by bars (like rectangle) whose lengths represent numerical values. One can use horizontal or vertical bars. Instead of rect… -
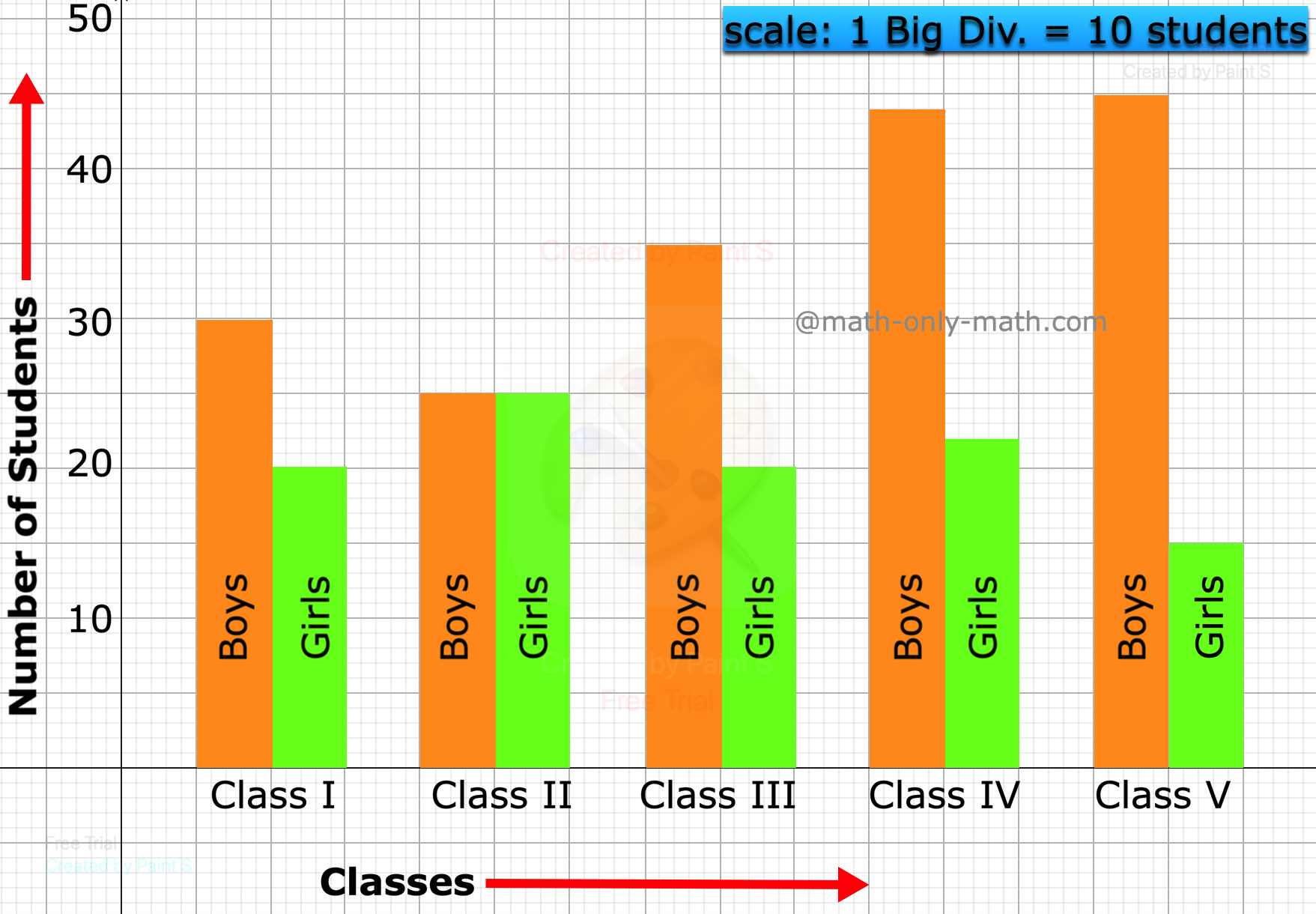
Construction of Bar Graphs | Examples on Construction of Column Graph
Jul 31, 25 03:35 AM
Now we will discuss about the construction of bar graphs or column graph. In brief let us recall about, what is bar graph? Bar graph is the simplest way to represent a data. In consists of rectangular… -
Successor and Predecessor | Successor of a Whole Number | Predecessor
Jul 29, 25 12:59 AM
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.