Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Rational Numbers
In mathematics, a rational number is a number which can be expressed as a fraction or a quotient, i.e., in the form of p/q where p and q are the two integers and ‘p’ is the numerator and ‘q’ is the non-zero denominator and p/q is in the lowest form, i.e. p and q have no common factors.
“Rational numbers (Q) are included in the real numbers, and in turn include the integers (Z), which include the natural numbers (N).” Thus, integers as well as fractions can be expressed in this form. So, all integers and fractions are rational numbers.
In p/q form q can be any number. So, q can also be equal to 1. When q = 1, every integer formed a rational number. Set of all rational number is denoted by ‘Q’.
Note: N ⊂ W ⊂ Z ⊂ Q
Some of the following are the examples of rational numbers:
(i) 2/3 is a rational number of form p/q where p = 2 and q = 3.
(ii) Similarly, 4/9 is a rational number of form p/q where p = 4 and q = 9.
(iii) 2 (i.e. 2/1) is a rational number of form p/q where p = 2 and q = 1. Also, 2 is a real number, a natural number, and an integer.
(iv) 0/5 (i.e. 0) is a rational number of form p/q where p = 0 and q = 5.
Arithmetical Operations on Rational numbers:
1. Addition of Rational Numbers:
(i) Addition of proper fractions:
1/2 + 3/2 = 4/2 = 2
4/9 + 5/9 = 9/9 = 1
(ii) Addition of improper fractions:
For addition of improper fractions we need to take LCM of the denominators and solve accordingly.
For Example:
2/3 + 2/5
= 2 x 5/15 + 2 x 3/15
= 10/15 + 6/15
= 16/15
2. Subtraction of Rational Numbers:
(i) For proper fractions:
5/9 - 4/9 = 1/9
(ii) For improper rational fractions:
Step involved will same as in case of addition of improper rational numbers
For example:
2/5 – 4/15
= 2 x 3/5 x 3 – 4/15
= 6/15 – 4/15
= 2/15
3. Multiplication of Rational Numbers:
For multiplication of proper or improper rational fraction process is same for both. The process id that numerator of both is multiplied and is divided by the product of both denominators.
For example:
(i) 3/7 x 4/7 = 12/49
(ii) 4/9 x 7/5 = 28/45
4. Division of Rational Numbers:
For example:
(i) Divide 4/6 with 2.
In above example both numerator and denominator will be separately divided by 2. After dividing we get the answer 2/3.
(ii) Divide 2/3 by 3/4:
In such cases questions will be solved as-
2/3 × 4/3 = 8/9
Rational Numbers
Decimal Representation of Rational Numbers
Rational Numbers in Terminating and Non-Terminating Decimals
Recurring Decimals as Rational Numbers
Laws of Algebra for Rational Numbers
Comparison between Two Rational Numbers
Rational Numbers Between Two Unequal Rational Numbers
Representation of Rational Numbers on Number Line
Problems on Rational numbers as Decimal Numbers
Problems Based On Recurring Decimals as Rational Numbers
Problems on Comparison Between Rational Numbers
Problems on Representation of Rational Numbers on Number Line
Worksheet on Comparison between Rational Numbers
Worksheet on Representation of Rational Numbers on the Number Line
9th Grade Math
From Rational Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
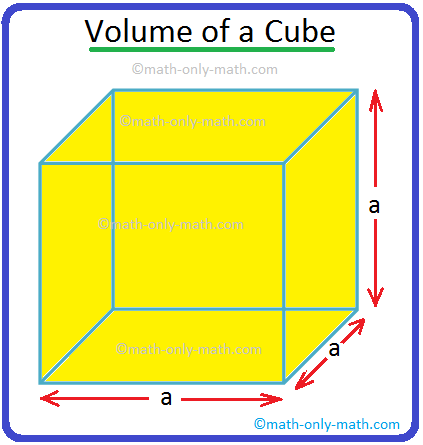
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 23, 25 11:37 AM
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
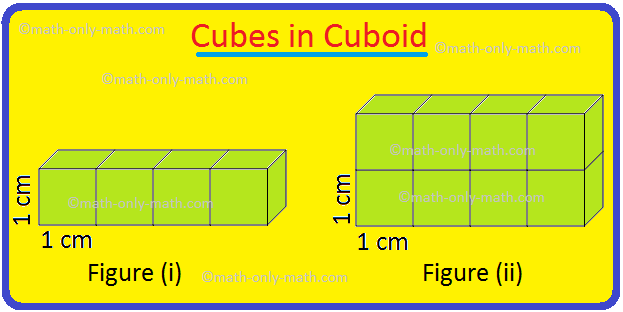
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 20, 25 12:58 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on… -
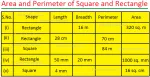
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
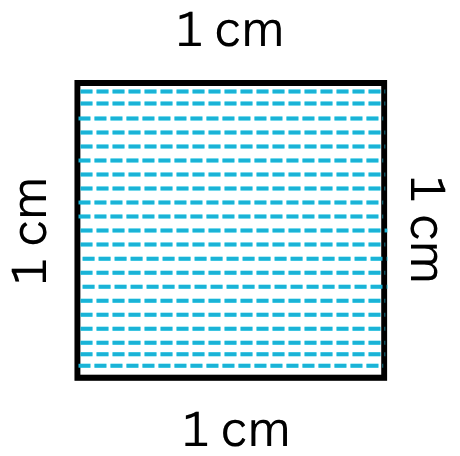
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.