Worksheet on H.C.F.

Practice the questions given in the worksheet on hcf (highest common factor) by factorization method, prime factorization method and division method.

I. Find the common factors of the following numbers.

(i) 6 and 8

(ii) 9 and 15 

(iii) 16 and 18

(iv) 16 and 28

(v) 51 and 68

(vi) 27 and 45

II. Find the common factors and the highest common factor of the given numbers. One has been solved to get the idea.

(i) 12 and 28

Factors of 12 = 1, 2, 3, 4, 6, 12

Factors of 28 = 1, 2, 4, 7, 14, 28

Common factors of 12 and 28 = 1, 2 and 4

Highest common factor (HCF) of 12 and 28 = 4

(ii) 15 and 12

(iii) 14 and 21

(iv) 18 and 24

(v) 40 and 50

III. Find the common factors for the numbers given below by circling the prime factors and then finding the HCF. First one is done for you as an example.

(i) 8 and 12

Prime factors of 8 = 2 × 2 × 2

Prime factors of 12 = 2 × 2 × 3

HCF of 8 and 12 = 2 × 2 = 4

(ii) 12 and 15

Prime factors of 12 =

Prime factors of 15 =

HCF of 12 and 15 =

(iii) 18 and 30

Prime factors of 18 =

Prime factors of 30 =

HCF of 18 and 30 =

(iv) 30 and 40

Prime factors of 30 =

Prime factors of 40 =

HCF of 30 and 40 =

(v) 56 and 42

Prime factors of 56 =

Prime factors of 42 =

HCF of 56 and 42 =

(vi) 27 and 63

Prime factors of 27 =

Prime factors of 63 =

HCF of 27 and 63 =

IV. Find the common factors and HCF of these numbers. First one is done for you as an example.

(i) 12 and 8

Factors of 12 = 1, 2, 3, 4, 6, 12

Factors of 8 = 1, 2, 4, 8

Common factors = 1, 2, 4

Highest common factors of 12 and 8 = 4

(ii) 10 and 6

(iii) 15 and 5

(iv) 20 and 15

(v) 8 and 10

(vi) 6 and 15

V. Which pairs are co-prime?

(i) 16, 18

(ii) 15, 14

(iii) 27, 28

(iv) 8, 15

(v) 11, 12

(vi) 45, 49

VI. Find the H.C.F. of the following by prime factorization method.

(i) 24 and 36

(ii) 56 and 72

(iii) 21 and 35

(iv) 56 and 70

(v) 45 and 81

(vi) 42 and 49

(vii) 44, 66 and 110

(viii) 48, 64 and 120

(ix) 12, 15 and 18

(x) 75 and 125

(xi) 64 and 78

(xii) 27, 36 and 54

VII. Find the H.C.F. of the following by factorization method.

(i) 16, 24

(ii) 28, 35

(iii) 48, 60

(iv) 15, 52, 65

(v) 15, 18, 30

(vi) 42, 54, 64

VIII. Find the H.C.F. of the following by Long Division Method.

(i) 32 and 68

(ii) 45 and 180

(iii) 56 and 72

(iv) 96 and 218

(v) 8, 16 and 36

(vi) 9, 18 and 27

(vii) 20, 80 and 128

(viii) 60, 80, 90

(ix) 25, 75, 95

(x) 12, 24, 88

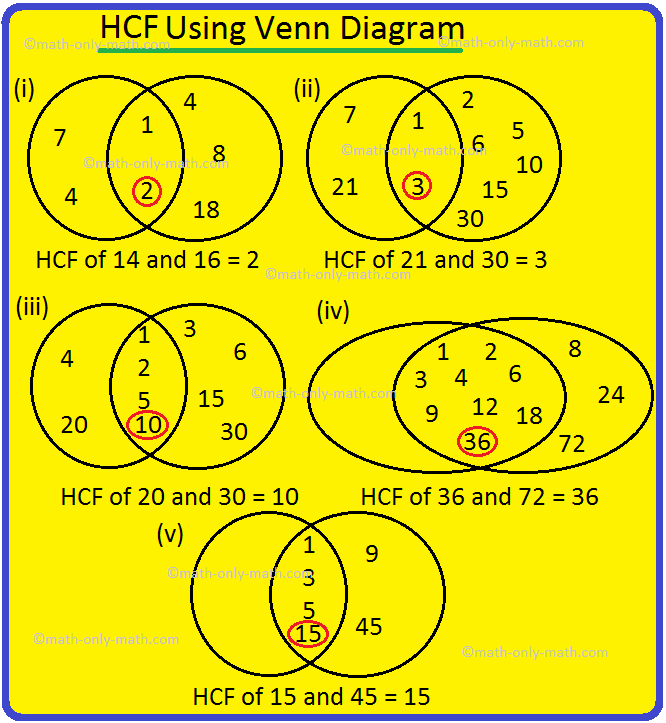
IX. Find the HCF of the given numbers using venn diagram.

(i) 14 and 16

(ii) 21 and 30

(iii) 20 and 30

(iv) 36 and 72

(v) 15 and 45

X. Find the highest common factor of the given numbers by long division method.

(i) 18 and 30

(ii) 75 and 180

(iii) 21 and 84

(iv) 108 and 288

(v) 12 and 54

(vi) 12, 30 and 54

XI. Fill in the blanks:

(i) The full form of H.C.F is …………………………..

(ii) The HCF of two prime numbers is always …………………………..

(iii) The HCF of 9 and 24 is …………………………..

(iv) The HCF of 12 and 18 is …………………………..

XII. A. Simplify the following using HCF.

(i) \(\frac{25}{65}\)

(ii) \(\frac{33}{99}\)

(iii) \(\frac{20}{72}\)

(iv) \(\frac{36}{60}\)

B. Find the HCF of

(i) 20 and 25

(ii) 4 and 6

(iii) 10 and 15

(iv) 15 and 20

(v) 16 and 40

(vi) 14 and 35

(viii) 16, 18 and 80

C. Find the HCF of the following numbers by long division method.

(i) 21, 35

(ii) 40, 75

(iii) 72, 84

(iv) 24, 64

(v) 96, 128

(vi) 27, 45

(vii) 24, 48

(viii) 60, 64

(ix) 17, 23

XIII. Multiple Choice Questions (MCQ) on Prime Factorization:

     Tick (✔) the correct option.

(i) The HCF of 144 and 180 is

(a) 78;     (b) 36;     (c) 45;     (d) 18

(ii) The HCF of 12, 18 and 27 is

(a) 6;     (b) 9;     (c) 1;     (d) 3

(iii) The HCF of two prime numbers is

(a) smaller of the two;     (b) greater of the two;     (c) 1;     (d) 0

XIV. Find the HCF of the following numbers by prime factorization method:

(i) 16 and 28

(ii) 15 and 20

(iii) 96 and 128

(iv) 504 and 980

(ν) 144 and 180

(vi) 2, 9 and 18

(vii) 50, 13 and 45

(viii) 12, 18 and 24

(ix) 14, 49 and 21

(x) 36, 27 and 45

XV. Find the HCF of the following numbers by division method:

(1) 130 and 150

(ii) 225 and 450

(iii) 54, 108 and 144

(iv) 144, 180 and 384

(ν) 120, 144 and 204

(vi) 101, 573 and 1079

Worksheet on Word Problems on H.C.F.

XVI. Solve the following.

(i) Two ropes are 64 cm and 80 cm long. What maximum length of pieces can be cutequally from the given ropes?

(ii) Find the greatest number which divides 8, 18 and 24 exactly.

(iii) Find the greatest number which is less by 1 to divide 15, 18 and 30 exactly.

(iv) Find the greatest number which is more by 5 to divide 12, 24 and 60 exactly.

(v) Find the greatest number which is less by 2 to divide 18, 36 and 45 exactly.

(vi) Find the greatest number which is more by 7 to divide 184, 230 and 276 exactly.

Answers for the worksheet on hcf are given below.

Answers:

I. (i) 2

(ii) 3 

(iii) 2

(iv) 2, 4

(v) 17

(vi) 3, 9

II. (ii) 3

(iii) 6

(iv) 10

(v) 14

(vi) 9

III. (ii) 1, 2, HCF = 2

(iii) 1, 5, HCF = 5

(iv) 1, 5, HCF = 5

(v) 1, 2, HCF = 2

(vi) 1, 3, HCF = 3

IV. (ii) 3

(iii) 7

(iv) 6

(v) 10

V. (ii) 15, 14

(iii) 27, 28

(iv) 8, 15

(v) 11, 12

(vi) 45, 49

VI. (i) 12

(ii) 8

(iii) 7

(iv) 14

(v) 9

(vi) 7

(vii) 22

(viii) 8

(ix) 3

(x) 25

(xi) 2

(xii) 9

VII. (i) 8

(ii) 7

(iii) 12

(iv) 1

(v) 3

(vi) 2

VIII. (i) 4

(ii) 45

(iii) 8

(iv) 2

(v) 4

(vi) 9

(vii) 4

(viii) 10

(ix) 5

(x) 4

IX. 

X. (i) 6

(ii) 15

(iii) 21

(iv) 36

(v) 6

(vi) 6

XI. (i) highest common factor

(ii) prime number

(iii) 3

(iv) 6

XII. A. (i) \(\frac{5}{13}\)

(ii) \(\frac{1}{3}\)

(iii) \(\frac{5}{18}\)

(iv) \(\frac{3}{5}\)

B. (i) 5

(ii) 2

(iii) 5

(iv) 5

(v) 8

(vi) 7

(viii) 2

C. (i) 7

(ii) 5

(iii) 12

(iv) 8

(v) 32

(vi) 9

(vii) 24

(viii) 4

(ix) 1

XIII. (i) (b) 36

(ii) (d) 3

(iii) (c) 1

XIV. (i) HCF of 16 and 28 is 4

(ii) HCF of 15 and 20 is 5

(iii) HCF of 96 and 128 is 32

(iv) HCF of 504 and 980 is 28

(ν) HCF of 144 and 180 is 36

(vi) HCF of 2, 9 and 18 is 1

(vii) HCF of 50, 13 and 45 is 1

(viii) HCF of 12, 18 and 24 is 6

(ix) HCF of 14, 49 and 21 is 7

(x) HCF of 36, 27 and 45 is 9

XV. (1) HCF of 130 and 150 is 10

(ii) HCF of 225 and 450 is 225

(iii) HCF of 54, 108 and 144 is 18

(iv) HCF of 144, 180 and 384 is 12

(ν) HCF of 120, 144 and 204 is 12

(vi) HCF of 101, 573 and 1079 is 1

XVI. (i) 16 cm

(ii) 2

(iii) 2

(iv) 17

(v) 7

(vi) 53

4th Grade Math Activities

From Worksheet on HCF to HOME PAGE