Use of Integers

The use of integers is used to express our day-to-day situations in Mathematical terms.

Examples:

(i) If profit are represented by positive integer then losses by negative integers.

(ii) If heights above sea level by positive integers then depths below sea level by negative integers.

(iii) If rise in price is represented by positive integers, then fall in price by negative integers and so on.

Thus, if +256 represent a profit of $ 256; then a loss of $ 256 is represented by -256.

Similarly, if a depth of 37 below sea level is represented by -37; then +37 represents a height of 37 above sea level and so on.

Use of integers as directed numbers:

When numbers represent direction, then numbers are called directed numbers.

For example:

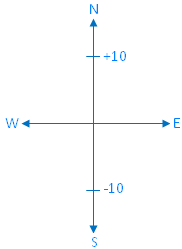
(i) If moving 10 m towards North is represented by +10;

-10 represents moving 10 m towards South, opposite direction of North.

If a positive (+ve) integer indicates a particular direction; then the negative (-ve) integer indicates the opposite direction. Conversely, if a negative (-ve) integer indicates any particular direction; then the positive (+ve) integer indicates the opposite direction.

For example:

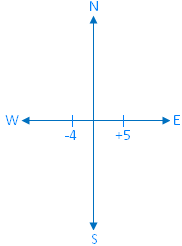
If +5 represents 5 m towards East; then -4 represents 4 m towards its opposite direction i.e., towards West.

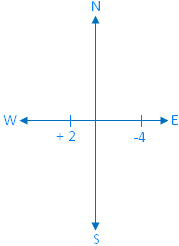
Similarly, if +9 represents 9 m due South, -6 represents 6 m due North. Again if -4 represents 4 km due East; +2 represents 2 km due West

(ii) If 12 m above the earth’s surface is represented by +12; then 18 m below the earth’s surface is represented by -18 and so on.

(iii) If +23 represents a profit of $23; then -19 represents a loss of $19.

(iv) If -63 indicate giving of $63; then taking of $91 is denoted by +91.

(v) If the rise in temperature by 63° C is denoted by +63; then -45 indicates the fall in temperature by 45° C

Write the opposite of the following expressions:

(i) An expenditure of $15.

(ii) A profit of $115.

(iii) A loss of $55.

(iv) Descending -15 m.

(v) Increase in weight by 17 kg.

Solution:

(i) Expenditure of $15 = Income of -15 dollars.

(ii) Profit of $115 = Loss of 115 dollars.

(iii) Loss of $55 = Profit of 55 dollars.

(iv) Descending -15 m or -15 m downwards movement = 15 m upward movement.

(v) Increase in weight by 17 kgs. = Decrease in weight by -17 kgs.

Numbers Page

6th Grade Page

From Use of Integers to HOME PAGE