Subscribe to our YouTube channel for the latest videos, updates, and tips.
Theorems on Locus of a Point which is Equidistant from Two Fixed Points
The locus of a point which is equidistant from two fixed points is the perpendicular bisector of the line segment joining the two fixed points.
Given,
Let X and Y be two given fixed points. PQ is the path traced out by the moving point P such that each point on it is equidistant from X and Y. Therefore, PX = PY.
To prove: PQ is the perpendicular bisector of the line segment XY.
Construction: Join X to Y. Let PQ cut XY at O.
Proof:
From △PXO and △PYO,
PX and PY (Given)
XO = YO (Since, every point of PQ is equidistant from X and Y, and O is a point on PQ.)
PO = PO (Common side.)
Therefore, by the SSS criterion of congruency△PXO ≅ △PYO.
Now ∠POX = ∠POY (since, corresponding parts of congruent triangles are congruent.)
Again ∠POX + ∠POY = 180° (Since, XOY is a straight line.
Therefore, ∠POX = ∠POY = 180°2 = 90°
Also, PQ bisects XY (Since, XO = YO)
Therefore, PQ ⊥ XY and PQ bisects XY, i.e., PQ is the perpendicular bisector of XY (Proved)
● Loci
From Theorems on Locus of a Point which is Equidistant from Two Fixed Points to HOME
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Average | Word Problem on Average | Questions on Average
May 17, 25 05:37 PM
In worksheet on average interest we will solve 10 different types of question. Find the average of first 10 prime numbers. The average height of a family of five is 150 cm. If the heights of 4 family -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate -
Worksheet on Rounding Off Number | Rounding off Number | Nearest 10
May 15, 25 05:12 PM
In worksheet on rounding off number we will solve 10 different types of problems. 1. Round off to nearest 10 each of the following numbers: (a) 14 (b) 57 (c) 61 (d) 819 (e) 7729 2. Round off to
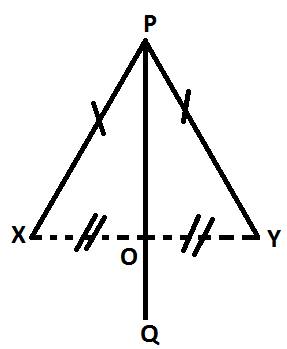
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.