Loci

We will discuss here about the basic concept of loci with two examples. 

Consider a point that is moving in a plane. If we join each of the positions through which the moving point passes, we will get the path followed by the point. If the movement of the point is random, its path will be irregular, and we shall not be able to predict, for example, how its path will look when the point stops. Therefore, the path of a randomly moving point cannot be determined. On the other hand, if the point’s movement obeys a given set of rules, the resulting path will be predictable and can be a circle, a straight line, an ellipse, and so on.

So, you can look upon a circle, a straight line, and so on, as a set of points positioned according to a given rule or rules.

Definition of locus: A path consisting of a set of points whose location is governed by some definite rule of rules is called locus. Locus in Latin means “position” or “location”.

Examples:

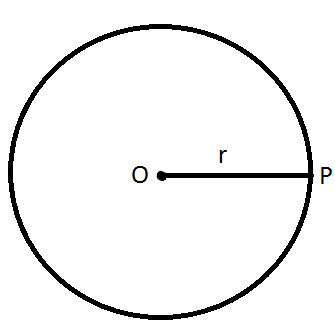
1. Let a point P move in such a way that it is always at a constant distance, r, from ma fixed point O.

The locus of a point P is a circle which has its center at O and has a radius equal to r units.

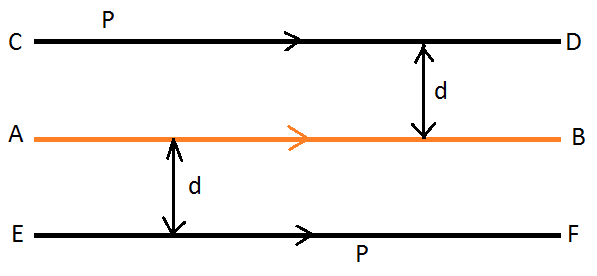
2. Suppose a point P moves so that it is at a constant distance d from a fixed straight line AB.

The locus of P consists of two straight lines, parallel to the fixed straight line AB, lying on both sides it at a distance of d units from it. Here, the locus of P is the pair of straight lines CD and EF.

● Loci

• Concept of loci
• Theorems on Locus of a Point which is Equidistant from Two Fixed Points

10th Grade Math

From Loci to HOME