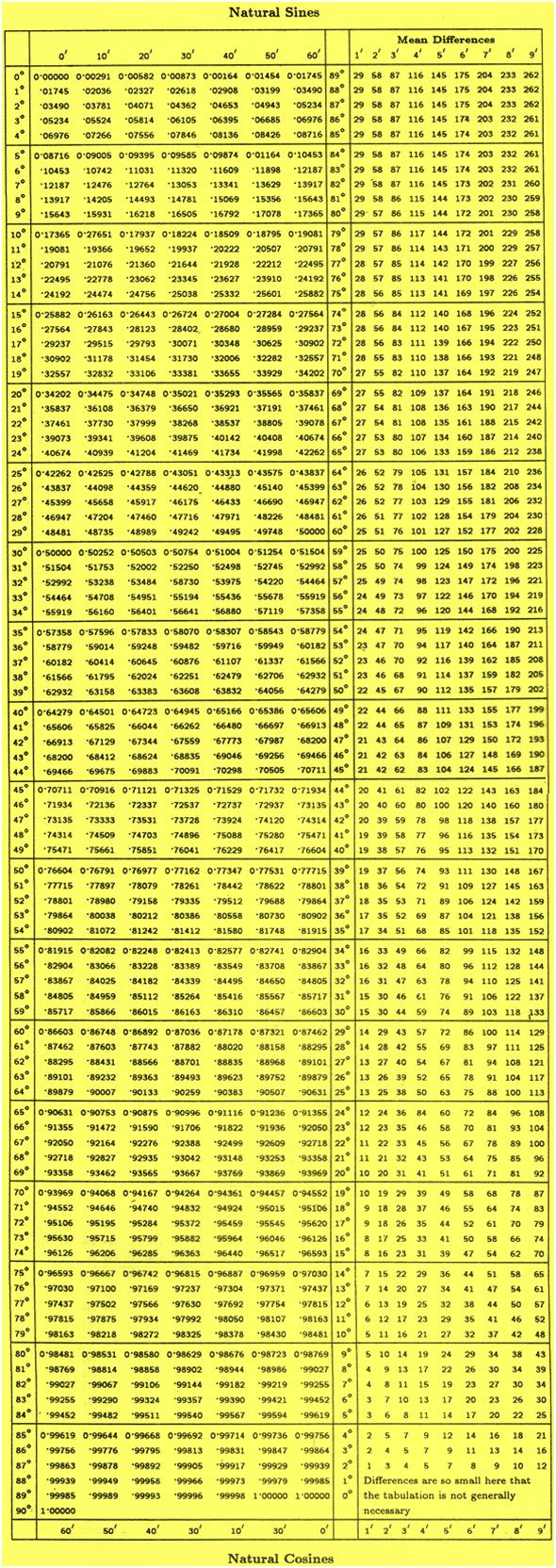
Table of Sines and Cosines

We will discuss here the method of using the table of sines and cosines:

This table shown below is also known as the table of natural sines and natural cosines.

Trigonometric Table of Sine and Cosine

Using the table we can find the values of sines and cosines of angles ranging from 0° to 90° at intervals of 1'.

We can observe that the table of natural sines and natural cosines are generally divided into the following parts. They are the following:

(i) In the extreme left vertical column of the table the angles are from 0° to 90° at intervals of 1°.

(b) In another vertical column about the middle of the table the angles are from 89° to 0° at intervals of 1°.

(ii) In the horizontal row at the top of the table the angles are from 0' to 60' at intervals of 10'.

(iii) In the horizontal row at the bottom of the table the angles are from 60' to 0' at intervals of 10'.

(iv) In the horizontal row at the extreme right of the table the angles are from 1' to 9' at intervals of 1'. This part of the table is known as Mean Difference Column.

Note:

(i) From the table we get the sine or cosine value of any given angle correct to five decimal places.

(ii) We know that the sine of any given angle is equal to that of cosine of its complementary  angle [i.e., sin  θ = cos (90 -  θ)]. So, the table is drawn in such a way that we can use the table to find the sin and cosine value of any given angle between 0° and 90°.

Solved examples using the table of natural sines and natural cosines:

1. Using table of natural sines, find the value of sin 55°.

Solution:

To find the value of sin 55° by the using the table of natural sines we need to go through the extreme left vertical column 0° to 90° and move downwards till we reach the angle 55°.

Then we move horizontally to the right at the top of the column headed by 0' and read the figure 0.81915, which is the require value of sin 55°.

Therefore, sin 55° = 0.81915

2. Using table of natural cosines, find the value of cos 29°

Solution:

To find the value of cos 29° by the using the table of natural cosines we need to go through the vertical column about the middle of the table 89° to 0° and move upwards till we reach angle 29°.

Then we move horizontally to the left at the bottom of the row above the column 0' and read the figure 0.87462, which is the require value of cos 29°.

Therefore, cos 29° = 0.87462

3. Using the trigonometric table, find the value of sin 62°30’

Solution:

To find the value of sin 62°30' by the using the table of natural sines we need to go through the extreme left vertical column 0° to 90° and move downwards till we reach the angle 62°.

Then we move horizontally to the right at the top of the column headed by 30' and read the figure 0.88701, which is the require value of sin 62°30'.

Therefore, sin 62°30' = 0.88701

4. Using table of natural sines and natural cosines, find the value of cos 63°50'   

Solution:

To find the value of cos 63°50' by the using the table of natural sines and natural cosines we need to go through the vertical column about the middle of the table 89° to 0° and move upwards till we reach angle 63°.

Then we move horizontally to the left at the bottom of the row above the column 50' and read the figure 0.44098, which is the require value of cos 63°50'.

Therefore, cos 63°50' = 0.44098

5. Using the trigonometric table, find the value of sin 33°28'

Solution:

To find the value of sin 33°28' by the using the trigonometric table table of natural sines we need to first find the value of sin 33°20'.

To find the value of sin 33°20’ by the using the table of natural sines we need to go through the extreme left vertical column 0° to 90° and move downwards till we reach the angle 33°.

Then we move horizontally to the right at the top of the column headed by 20' and read the figure 0.54951, which is the require value of sin 33°20'.

Therefore, sin 33°20' = 0.54951

Now we move further right along the horizontal line of angle 33° to the column headed by 8' of mean difference and read the figure 194 there; this figure of the table does not contain decimal sign. In fact, 194 implies 0.00194. Now we know that when the value of an angle increases from 0° to 90°, its sine value increases continually from 0 to 1. Therefore, to find the value of sin 33°28' we need to add the value corresponding to 8’ with the value of sin 33°20'.

Therefore, sin 33°28' = sin (sin 33°20' + 8') = 0.54951 + 0.00194 = 0.55145

6. Using the trigonometric table, find the value of cos 47°56'

Solution:

To find the value of cos 47°56' by the using the trigonometric table table of natural sines and natural cosines we need to first find the value of cos 47°50'

To find the value of 47°50' by the using the table of natural sines and natural cosines we need to go through the vertical column about the middle of the table 89° to 0° and move upwards till we reach angle 47°.

Then we move horizontally to the left at the bottom of the row above the column 50’ and read the figure 0.67129, which is the require value of cos 47°50'.

Therefore, cos 47°50' = 0.67129

Now we move further right along the horizontal line of angle 47° to the column headed by 6’ of mean difference and read the figure 129 there; this figure of the table does not contain decimal sign. In fact this figure 60 implies 0∙ 00129. We know that when the value of an angle increases from 0° to 90°, its cosines value decreases continually from 1 to 0. Therefore, to find the value of cos 47°56' we need to subtract the value corresponding to 6' from the value of cos 47°50'

Therefore, cos 47°56' = cos (47°50' + 6') = 0.67129 - 0∙ 00129 = 0.67

● Trigonometrical Table

• Table of Sines and Cosines
• Table of Tangents and Cotangents

11 and 12 Grade Math

From Table of Sines and Cosines to HOME PAGE