Subscribe to our YouTube channel for the latest videos, updates, and tips.
Learn to Write Number 4
Learn to write number 4 in preschool math activities for kids.
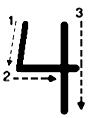
How to write number 4?
four
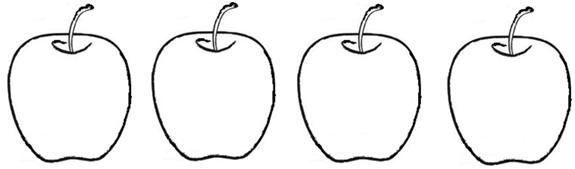
Color the above apples so that kids can identify the number and also understand the basic counting.
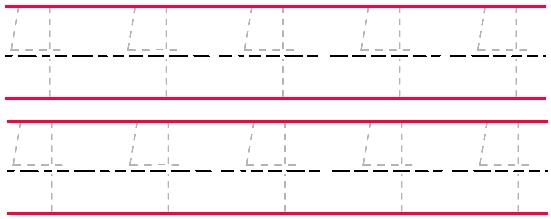
Trace the numbers:
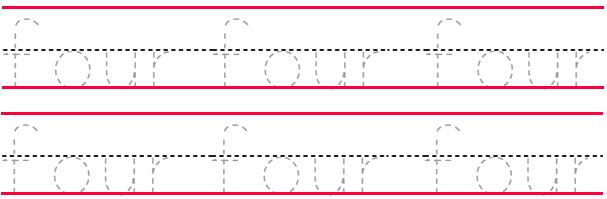
Trace the numbers in words:
In this worksheet kids can enjoy both coloring as well as tracing numbers.
Preschoolers and homeschoolers can enjoy practicing these colorful printable preschool worksheets on numbers to make the kids handwriting perfect. Parents and teachers can take the printouts of these worksheets on numbers for kids and help the kids to practice these worksheets which are absolutely free. Take as many printouts you want so that kids can practice tracing the numbers and also enjoy coloring as many they want. These printable math worksheets for kids can be access by anyone from anywhere. Trace the numbers carefully so that kids can learn to write number on their own.
Math Only Math is based on the premise that children do not make a distinction between play and work and learn best when learning becomes play and play becomes learning.
However, suggestions for further improvement, from all quarters would be greatly appreciated.
Learn to Write Number 1.
Learn to Write Number 2.
Learn to Write Number 3.
Learn to Write Number 4.
Learn to Write Number 5.
Learn to Write Number 6.
Learn to Write Number 7.
Learn to Write Number 8.
Learn to Write Number 9.
Learn to Write Number 10.
Preschool Math Activities
From Learn to Write Number 4 to HOME PAGE
Recent Articles
-
Terms Related to Simple Interest | Simple Interest Formula | Principal
Jun 18, 25 02:57 PM
In terms related to simple interest we will learn all the terms related to simple interest. The terms related to simple interest are Interest, Principal, Amount, Simple Interest, Time or period of tim… -
Introduction to Simple Interest | Definition | Formula | Examples
Jun 18, 25 01:50 AM
In simple interest we will learn and identify about the terms like Principal, Time, Rate, Amount, etc. PRINCIPAL (P): The money you deposit or put in the bank is called the PRINCIPAL. -
5th Grade Profit and Loss Percentage Worksheet | Profit and Loss | Ans
Jun 18, 25 01:33 AM
In 5th grade profit and loss percentage worksheet you will get different types of problems on finding the profit or loss percentage when cost price and selling price are given, finding the selling pri… -
Worksheet on Profit and Loss | Word Problem on Profit and Loss | Math
Jun 18, 25 01:29 AM
In worksheet on profit and loss, we can see below there are some different types of questions which we can practice in our homework. -
Calculating Profit Percent and Loss Percent | Profit and Loss Formulas
Jun 15, 25 04:06 PM
In calculating profit percent and loss percent we will learn about the basic concepts of profit and loss. We will recall facts and formula while calculating profit percent and loss percent. Now we wil
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.