Height and Distance with Two Angles of Elevation

We will solve different types of problems on height and distance with two angles of elevation.

Another type of case arises for two angles of elevations.

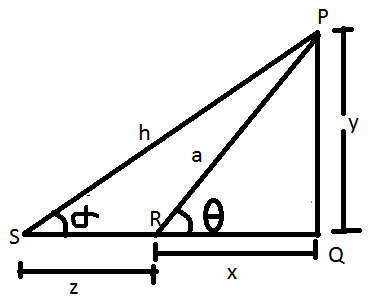
In the given figure, let

PQ be the height of pole of ‘y’ units.

QR be the one of the distance between the foot of the pole and one of the observer’s point with QR = ‘x’ units.

QS be the another distance between the foot of pole and other observer’s point with QR = ‘z + x’ units.

PR be the one of the line of sight as ‘a’ units and PS be the line of sight as ‘h’ units.

Let ‘θ’ be one the angle of elevation whose line of sight is PR and ‘α’ be the angle of elevation whose line of sight is PS.

Now the trigonometric formulae becomes,

          sin θ = $\frac{y}{a}$; cosec θ = $\frac{a}{y}$

          cos θ = $\frac{x}{h}$; sec θ = $\frac{h}{x}$

          tan θ = $\frac{y}{x}$; cot θ = $\frac{x}{y}$.

          sin α = $\frac{y}{h}$; cosec α = $\frac{h}{y}$

          cos α = $\frac{z + x}{h}$; sec α = $\frac{h}{z + x}$

          tan α = $\frac{y}{z + x}$; cot α = $\frac{z + x}{y}$

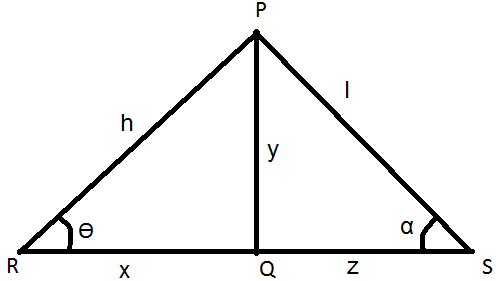
Another similar type of case for two angles of elevation is that when two people are looking at the same tower from two opposite sides.

Let PQ be the tower of length ‘y’ units.

RQ be the distance between foot of tower and one of the observer’s position of ‘x’ units.

QS be the distance between foot of tower and another observer’s position of ‘z’ units.

PR be the one of the line of sight of ‘h’ units.

PS is the line of sight of ‘l’ units.

Then, according to trigonometry,

sin θ = $\frac{PQ}{PR}$ = $\frac{y}{h}$; cosec θ = $\frac{PR}{PQ}$ = $\frac{h}{y}$

cos θ = $\frac{QR}{PR}$ = $\frac{x}{h}$; sec θ = $\frac{PR}{QR}$ = $\frac{h}{x}$

tan θ = $\frac{PQ}{QR}$ = $\frac{y}{x}$; cot θ = $\frac{QR}{PQ}$ = $\frac{x}{y}$

sin α = $\frac{PQ}{PS}$ = $\frac{y}{l}$; cosec α = $\frac{PS}{PQ}$ = $\frac{l}{y}$

cos α = $\frac{QS}{PS}$ = $\frac{z}{l}$; sec α = $\frac{PS}{QS}$ = $\frac{l}{z}$

tan α = $\frac{PQ}{PS}$ = $\frac{y}{z}$; cot α = $\frac{PS}{PQ}$ = $\frac{z}{y}$.

Now, let us solve some examples based upon above explained concept.

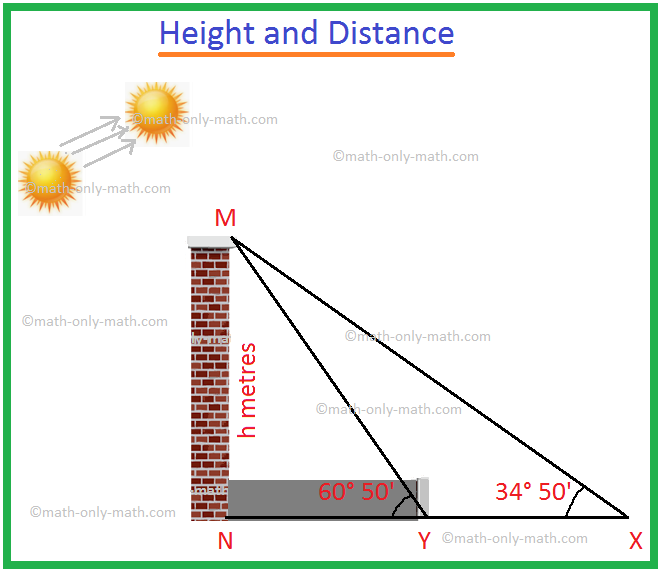
1. When the angle of elevation of the sum increases from 34° 50' to 60° 50', the length of the shadow of a tower reduces by 60 metres. Find the height of the tower.

Solution:

Let MN be the tower of height h metres.

The shadow of MN is NX when the angle of elevation of the sun is ∠MXN = 34° 50'.

The shadow of MN is NY when the angle of elevation of the sun is ∠MYN = 60° 50'.

Given that the reduction in the length of shadow = XY = 60 m.

From the right-angled triangle MXN, 

$\frac{h}{XN}$ = tan 34° 50'

Lets try to find the value of tan 34° 50' from the trigonometric table of natural tangents.

To find the value of tan 34° 50', look at the extreme left column. Start from the top and move downwards till you reach 34.

Now, move to the right in the row of 34 and reach the column of 48′.

We find 6950 i.e., 0.6950

So, tan 34° 50′ = 0.6950 + mean difference for 2′

                       = 0.6950

                       +         9  [Addition, because tan 34° 50′ > tan 34° 48′]

                          0.6959

Therefore, tan 34° 50′ = 0.6959.

Thus, $\frac{h}{XN}$ = 0.6959.

⟹ XN = $\frac{h}{0.6959}$ ................................... (i)

Again, from the right-angled triangle MYN,

$\frac{h}{YN}$ = tan 60° 50'

Let's try to find the value of tan 60° 50' from the trigonometric table of natural tangents.

To find the value of tan 60° 50', look at the extreme left column. Start from the top and move downwards till you reach 60.

Now, move to the right in the row of 60 and reach the column of 48′.

We find 7893 i.e., 0.7893

So, tan 60° 50′ = 0.7893 + mean difference for 2′

                       = 0.7893

                      +         24  [Addition, because tan 60° 50′ > tan 60° 48′]

                           0.7917

Therefore, tan 60° 50′ = 0.7917.

Thus, $\frac{h}{YN}$ = 0.7917.

⟹ YN = $\frac{h}{0.7917}$ ................................... (ii)

Now subtracting (ii) from (i) we get, 

XN - YN = $\frac{h}{0.6959}$ - $\frac{h}{0.7917}$

⟹ XY = h($\frac{1}{0.6959}$ - $\frac{1}{0.7917}$)

⟹ 60 = h($\frac{1}{0.7}$ - $\frac{1}{0.8}$), [Approx.]

⟹ 60 = h ∙ $\frac{1.1}{0.7 × 0.8}$

⟹ h = $\frac{60 × 0.7 × 0.8}{1.1}$

⟹ h = 68.73.

Hence, the height of the tower = 68.73 m (Approx.).

2. A man is standing at a distance of 10 m from a tower of height 20 m to left of it. Find the angle of elevation when the man looks to the top most point of the tower. Another man is standing at a distance of 40 m from the foot of the tower on the same side. Find the angle of elevation in this case.

Solution:

The problem can be visualized as:

In the problem, we are given,

Height of tower, PQ = y = 20 m

Distance tower’s foot and one of the observer, QR = x = 10 m

Distance between tower’s foot and another observer, QS = z = 40 m.

We know that:

tan θ = $\frac{y}{x}$

⟹ tan θ = $\frac{20}{10}$

⟹ tan θ = 2

⟹ θ = tan-1 (2)

⟹ θ = 63.43°.

Also, we know that:

tan α = $\frac{y}{z + x}$

⟹ tan α = $\frac{20}{40}$

⟹ tan α = $\frac{2}{4}$

⟹ tan α = ½

⟹ α = tan^-1($\frac{1}{2}$)

⟹ α = 26.56°

3. An observer is standing in front of a tower of height 30 m and the angle of elevation made by the eyes of observer is 56°. Another observer is standing at the opposite side of the tower and the angle of elevation in this case is 60°. then, find:

(i) distance between foot of tower and first observer.

(ii) Distance between foot of tower and second observer.

Solution:

The given problem can be visualized as:

In the given problem, we are known that;

Height of tower, PQ = y = 30m

Angle of elevation for first observer, θ = 56°

Angle of elevation for second observer, α = 60°

From trigonometric equations, we know that:

tan θ = $\frac{PQ}{QR}$ = $\frac{y}{x}$

⟹ tan θ = $\frac{PQ}{QR}$ = $\frac{30}{x}$.

⟹ tan θ = $\frac{30}{x}$

⟹ tan(56°) = $\frac{30}{x}$

⟹ 1.48 = $\frac{30}{x}$

⟹ x = $\frac{30}{1.48}$

⟹ x = 20.27

Hence distance between foot of tower and first observer = 20.27 m.

also, we know that;

tan α = $\frac{PQ}{PS}$ = $\frac{y}{z}$

⟹ tan α = $\frac{30}{z}$

⟹ tan (60°) = $\frac{30}{z}$

⟹ 1.732 = $\frac{30}{z}$

⟹ z = $\frac{30}{1.732}$

⟹ z = 17.32

Hence, distance between foot of tower and 2nd observer is 17.32 m.

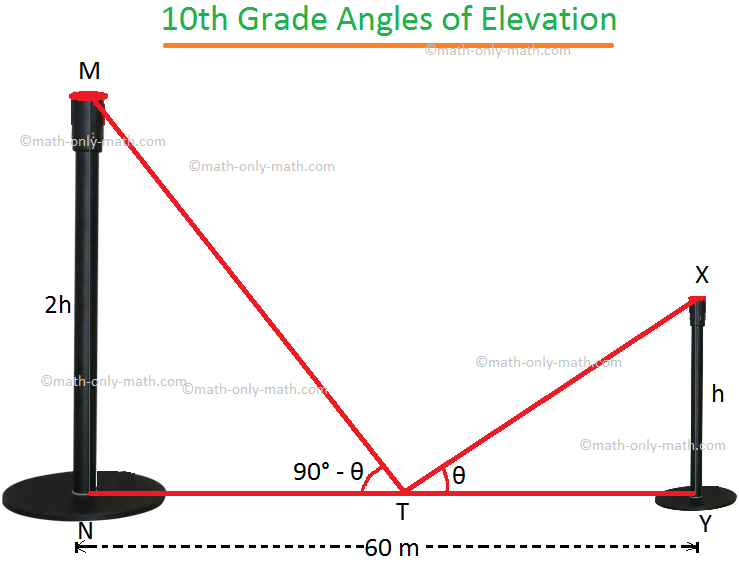
4. The distance between two vertical poles is 60 m. The height of one of the pole is double the height of the other. The angles of elevation of the tops of the poles from the middle point of the line segment joining their feet are complementary to each other. Find the heights of the poles. 

Solution:

Let MN and XY be the two poles.

Let XY = h.

therefore, according to the problem MN = 2h. T is the midpoint of NY, where NY = 60 m.

Therefore, NT = TY = 30 m.

If ∠XTY = θ then from the question, ∠MTN = 90° - θ.

In the right-angled ∆XYT,

tan θ = $\frac{XY}{TY}$ = $\frac{h}{30 m}$.

Therefore, h = 30 ∙ tan θ m .............................. (i)

In the right-angled ∆MNT,

tan (90° - θ) = $\frac{MN}{NT}$ = $\frac{2h}{30 m}$.

Therefore, cot θ = $\frac{2h}{30 m}$.

⟹ h = 15 ∙ cot θ m .............................. (ii)

Multiplying (i) and (ii) we get, 

h^2 = (30 ∙ tan θ × 15 ∙ cot θ) m^2

⟹ h^2 = 450 m^2

⟹ h = $\sqrt{450}$ m

⟹ h = 21.21 m (Approx.)

Therefore, the heights of the poles are 21.21 m (Approx.) and 42.42 m (Approx.) 

10th Grade Math

From Height and Distance with Two Angles of Elevation to HOME