Division of Algebraic Expression

In division of algebraic expression if x is a variable and m, n are positive integers such that m > n then (xᵐ ÷ xⁿ) = x\(^{m - n}\).

I. Division of a Monomial by a Monomial

Quotient of two monomials is a monomial which is equal to the quotient of their numerical coefficients, multiplied by the quotient of their literal coefficients.

Rule:

Quotient of two monomials = (quotient of their numerical coefficients) x (quotient of their variables)

Divide:

(i) 8x²y³ by -2xy

Solution:

(i) 8x²y³/-2xy

= (⁸/_-2) x^{2 - 1}y^{3 - 1} [Using quotient law x^m ÷ xⁿ = x^{m - n}]

= -4xy².




(ii) 35x³yz² by -7xyz

Solution:

35x³yz² by -7xyz

= (³⁵/_-7) x^{3 - 1}y^{1 - 1}z^{2 - 1} [Using quotient law x^m ÷ xⁿ = x^{m - n}]

= -5 x²y⁰z¹ [y⁰ = 1]

= -5x²z.


(iii) -15x³yz³ by -5xyz²

Solution:

-15x³yz³ by -5xyz².

= (^-15/_-5) x^{3 - 1}y^{1 - 1}z^{3 - 2}. [Using quotient law x^m ÷ xⁿ = x^{m - n}].

= 3 x²y⁰z¹ [y⁰ = 1].

= 3x²z.

II. Division of a Polynomial by a Monomial

Rule:

For dividing a polynomial by a monomial, divide each term of the polynomial by the monomial. We divide each term of the polynomial by the monomial and then simplify.

Divide:

(i) 6x⁵ + 18x⁴ - 3x² by 3x²

Solution:

6x⁵ + 18x⁴ - 3x² by 3x²

= (6x⁵ + 18x⁴ - 3x²) ÷ 3x² 6x⁵/3x² + 18x⁴/3x² - 3x²/3x²

=2x³ + 6x² - 1.


(ii) 20x³y + 12x²y² - 10xy by 2xy

Solution:

20x³y + 12x²y² - 10xy by 2xy

= (20x³y + 12x²y² - 10xy) ÷ 2xy

= 20x³y/2xy + 12x²y²/2xy - 10xy/2xy

= 10x² + 6xy - 5.

III. Division of a Polynomial by a Polynomial

We may proceed according to the steps given below:

(i) Arrange the terms of the dividend and divisor in descending order of their degrees.

(ii) Divide the first term of the dividend by the first term of the divisor to obtain the first term of the quotient.

(iii) Multiply all the terms of the divisor by the first term of the quotient and subtract the result from the dividend.

(iv) Consider the remainder (if any) as a new dividend and proceed as before.

(v) Repeat this process till we obtain a remainder which is either 0 or a polynomial of degree less than that of the divisor.

Let us understand it through some examples.

1. Divide 12 – 14a² – 13a by (3 + 2a).

Solution:

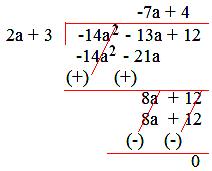
12 – 14a² – 13a by (3 + 2a).

Write the terms of the polynomial (dividend and divisor both) in decreasing order of exponents of variables.

So, dividend becomes – 14a² – 13a + 12 and divisor becomes 2a + 3.

Divide the first term of the dividend by the first term of the divisor which gives first term of the quotient.

Multiply the divisor by the first term of the quotient and subtract the product from the dividend which gives the remainder.

Now, this remainder is treated as, new dividend but the divisor remains the same.

Now, we divide the first term of the new dividend by the first term of the divisor which gives second term of the quotient.

Now, multiply the divisor by the term of the quotient just obtained and subtracts the product from the dividend.

Thus, we conclude that divisor and quotient are the factors of dividend if the remainder is zero.

Quotient = -7a + 4

Remainder = 0

Verification:

Dividend = divisor × quotient + remainder

= (2a + 3)(-7a + 4) + 0

= 2a(-7a + 4) +3(-7a + 4) + 0

= – 14a² + 8a – 21a + 12 + 0

= – 14a² – 13a + 12

2. Divide 2x² + 3x + 1 by (x + 1).

Solution:

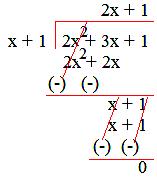
Therefore, quotient = (2x + 1) and remainder = 0.

3. Divide x² + 6x + 8 by (x + 4).

Solution:

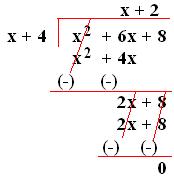
Therefore, Dividend = x² + 6x + 8

Divisor = x + 4

Quotient = x + 2 and

Remainder = 0.

4. Divide 9x - 6x² + x³ - 2 by (x - 2).

Solution:

Arranging the terms of the dividend and divisor in descending order and then dividing,

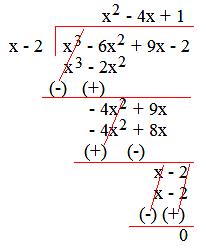
Therefore, quotient = (x² - 4x + 1) and remainder = 0.

5. Divide (29x - 6x² - 28) by (3x -4).

Solution:

Arranging the terms of the dividend and divisor in descending order and then dividing,

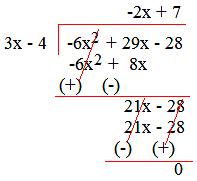
Therefore, (29x - 6x² - 28) ÷ (3x - 4) = (-2x + 7).

6. Divide (5x³ - 4x² + 3x + 18) by (3 - 2x + x²).

Solution:

The terms of the dividend are in descending order.

Arranging the terms of the divisor in descending order and then dividing,

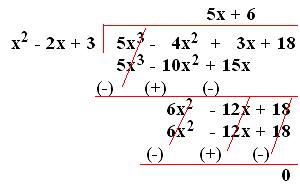
Therefore, (5x³ - 4x² + 3x + 18) ÷ (x² - 2x + 3) = (5x + 6).

7. Using division, show that (x - 1) is a factor of (x³ - 1).

Solution:

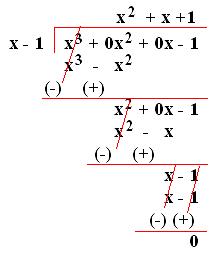
(x - 1) completely divides (x³ - 1).

Hence, (x - 1) is a factor of(x³- 1).

8. Find the quotient and remainder when (7 + 15x - 13x² + 5x³) is divided by (4 - 3x + x²).

Solution:

Arranging the terms of dividend and divisor in descending order and then dividing,

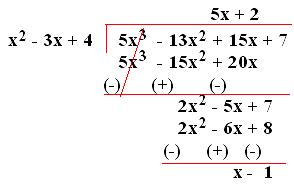
Therefore, quotient is (5x + 2) and remainder is (x - 1).

9. Divide (10x⁴ + 17x³ - 62x² + 30x - 3) by (2x² + 7x - 1).

Solution:

The terms of the dividend and that of the divisor are in descending order. So, we divide them as;

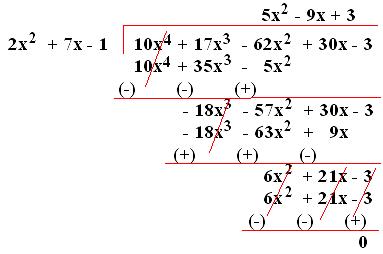
(10x⁴ + 17x³ - 62x² + 30x - 3) ÷ (2x² + 7x - 1) = (5x² - 9x + 3).

● Algebraic Expression

Algebraic Expression

Addition of Algebraic Expressions

Subtraction of Algebraic Expressions

Multiplication of Algebraic Expression

Division of Algebraic Expressions

8th Grade Math Practice

From Division of Algebraic Expression to HOME PAGE