Theorem of Three Perpendiculars
Theorem of three perpendiculars is explained herewith some specific examples.
Theorem: If PQ is perpendicular to a plane XY and if from Q, the foot of the perpendicular, a straight line QR is drawn perpendicular to any straight line ST in the plane, then PR is also perpendicular to ST.
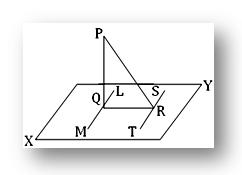
Construction: Through Q draw in the plane XY the straight line LM parallel to ST.
Proof: Since LM is parallel to ST and QR perpendicular to ST hence, QR is perpendicular to LM. Again, PQ is perpendicular to the plane XY; hence, it is perpendicular to the line LM. Therefore, LM is perpendicular to both PQ and QR at Q. This implies LM is perpendicular to the plane PQR. Now, ST and LM are parallel and LM is perpendicular to the plane PQR; hence, ST is perpendicular to the plane PQR. Therefore, ST is perpendicular to PR or in other words, PR is perpendicular to ST.
Example:
1. Straight lines in space which are parallel to a given straight line are parallel to one another.
Let AB and CD be two straight lines each of which is parallel to the given line LM. We are to prove that the straight lines AB and CD are parallel to each other.
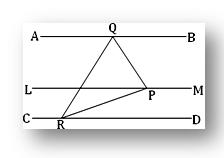
Construction: Draw a plane PQR perpendicular to LM and let us assume that the drawn plane cuts LM, AB and CD at P, Q and R respectively.
Proof: By hypothesis AB is parallel to LM and by construction LM is perpendicular to the plane PQR. Therefore, AB is also perpendicular to the plane PQR. Similarly, CD is also perpendicular to the same plane. Thus, each of AB and CD is perpendicular to the same plane PQR. Therefore, the straight lines AB and CD are parallel to one another.
2. Prove that the quadrilateral formed by joining the middle points of the adjacent sides of a skew quadrilateral is a co-planar parallelogram.
Let W, X, Y and Z be the mid-points of the sides AB, BC, CD and DA of a skew quadrilateral ABCD. We are to prove that, the quadrilateral WXYZ is a co-planar parallelogram.
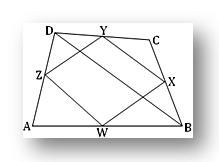
Construction: Join WX, XY, YZ, WZ and BD.
Proof: Wand Z are the mid-points of the sides AB and AD respectively in the plane △ ABD. Therefore, ZW is parallel to BD and ZW = 1/2 BD. Similarly, X and Y are the mid-points of the sides BC and CD respectively in the plane △ BCD. Therefore, XY is parallel to BD and XY = 1/2 BD. Since both of ZW and XY are parallel to BD, hence they are parallel to one another. Therefore, there is a plane passing through ZW and YX.
Similarly, WX and ZY are parallel to each other and therefore, there is a plane passing through WX and ZY. Both the planes through ZW and YX and through WX and ZY pass through four points W, X, Y and Z. Therefore, it is evident that the two planes must be the same. Hence, the quadrilateral WXYZ is co-planar. Again, ZW is parallel to YX and ZW = YX. Therefore, the quadrilateral WXYZ is a parallelogram.
● Geometry
- Solid Geometry
- Worksheet on Solid Geometry
- Theorems on Solid Geometry
- Theorems on Straight Lines and Plane
- Theorem on Co-planar
- Theorem on Parallel Lines and Plane
- Theorem of Three Perpendiculars
- Worksheet on Theorems of Solid Geometry
11 and 12 Grade Math
From Theorem of Three Perpendiculars to HOME PAGE
Recent Articles
-
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
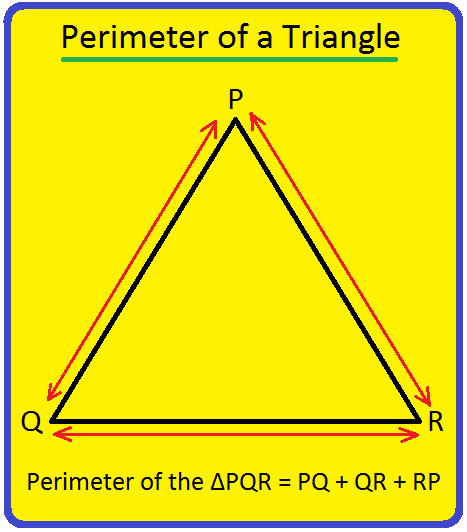
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
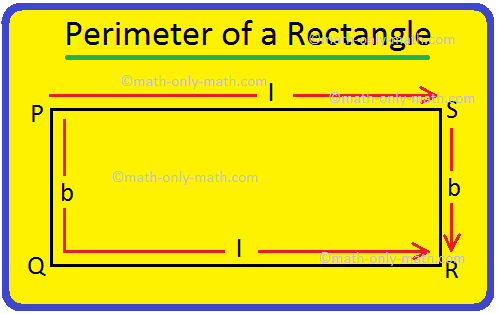
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.