Prime Factorisation
Prime factorisation or complete factorisation of the given number is to express a given number as a product of prime factor.
When a number is expressed as the product of its prime factors, it is called prime factorization.
For example, 15 = 3 × 5. So, 3 and 5 are prime factors of 15.
Prime factors of a number are always the prime numbers, when a number is expressed as product of prime numbers, it is called prime factorization. Prime factorization can be done, using two methods: division method and factor tree method.
HCF of two or more numbers can be obtained by prime factorization. To find the HCF by prime factorization, we first find all the prime factors of the given numbers and then find the product of all the common prime factors. The product is the HCF of the given numbers.
Factor Tree Method:
We write pairs of factors for the given number in circles which make branches of a factor tree.
Division Method:
Divide the given numbers by the smallest prime number. Continue the division until it is not further divisible. Factorisation stops when we reach a prime number.
Observe the following examples of Prime factorisation in two methods i.e., Factor Tree Method and Division Method.
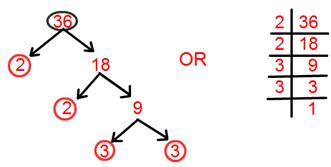
1. Find prime factorisation of 36.
Prime factorisation of 36 = 2 × 2 × 3 × 3.
= 2² × 3².
[Here two ways to solve factorisation one is tree factorisation method and the other one is by dividing.]
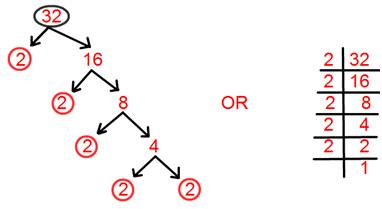
2. Find prime factorisation of 32.
Solution:
Prime factorisation of 32 = 2 × 2 × 2 × 2 × 2.
= 2⁵.
3. Find prime factorisation of 51.
Solution:
Prime factorisation of 51 = 3 × 17.
= 3¹ × 17¹
= 3 × 17.
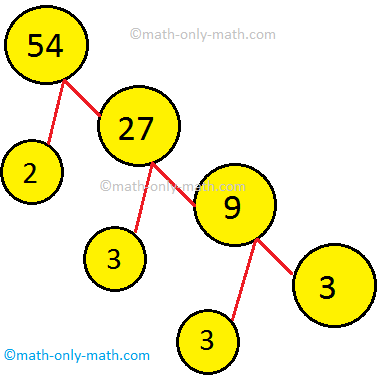
4. Draw a factor tree to show the prime factorization of 54.
Solution:
5. Find prime factorisation of 57.
Solution:
Prime factorisation of 57 = 3 × 19
= 3¹ × 19¹
= 3 × 19.
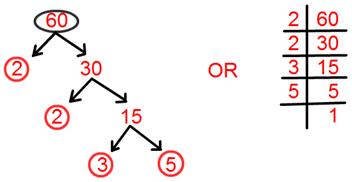
6. Find prime factorisation of 60.
Solution:
Prime factorisation of 60 = 2 × 2 × 3 × 5.
= 2² × 3 × 5.
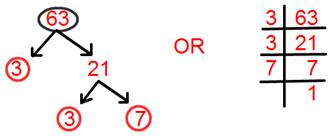
7. Find prime factorisation of 63.
Solution:
Prime factorisation of 63 = 3 × 3 × 7.
= 3² × 7.
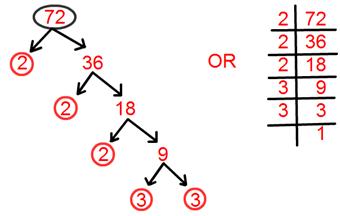
8. Find prime factorisation of 72.
Solution:
Prime factorisation of 72 = 2 × 2 × 2 × 3 × 3.
= 2³ × 3².
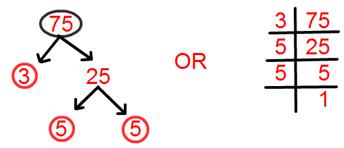
9. Find prime factorisation of 75.
Solution:
Prime factorisation of 75 = 3 × 5 × 5.
= 3 × 5².
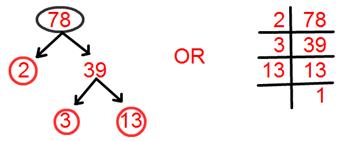
10. Find prime factorisation of 78.
Solution:
Prime factorisation of 78 = 2 × 3 × 13.
11. Find prime factorisation of 93.
Solution:
Prime factorisation of 93 = 3 × 31.
12. Find prime factorisation of 102.
Solution:
Prime factorisation of 102 = 2 × 3 × 17.
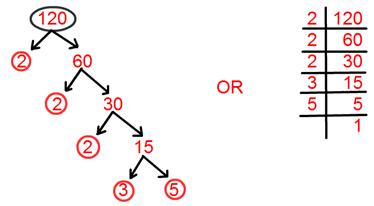
13. Find prime factorisation of 120.
Solution:
Prime factorisation of 120 = 2 × 2 × 2 × 3 × 5.
= 2³ × 3 × 5.
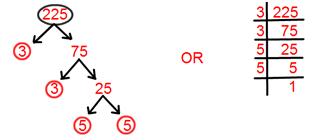
14. Find prime factorisation of 225.
Solution:
Prime factorisation of 225 = 3 × 3 × 5 × 5.
= 3² × 5².
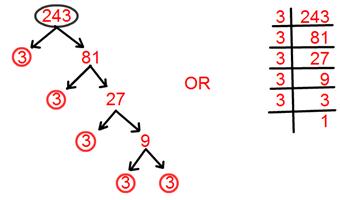
15. Find prime factorisation of 243.
Solution:
Prime factorisation of 243 = 3 × 3 × 3 × 3 × 3.
= 3⁵.
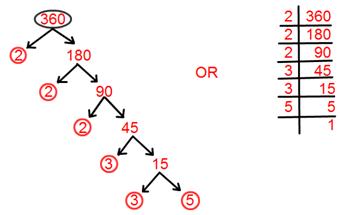
16. Find prime factorisation of 360.
Solution:
Prime factorisation of 360 = 2 × 2 × 2 × 3 × 3 × 5.
= 2³ × 3² × 5.
Questions and Answers on Prime Factorisation:
I. Find the prime factors of the given number through prime factorization. First one is shown as an example for you.
(i) 144
(ii) 81
(iii) 72
(iv) 48
(v) 100
(vi) 64
(vii) 108
(viii) 248
(ix) 256
● Factors.
● Highest Common Factor (H.C.F).
● Examples on Highest Common Factor (H.C.F).
● Greatest Common Factor (G.C.F).
● Examples of Greatest Common Factor (G.C.F).
● To find Highest Common Factor by using Prime Factorization Method.
● Examples to find Highest Common Factor by using Prime Factorization Method.
● To find Highest Common Factor by using Division Method.
● Examples to find Highest Common Factor of two numbers by using Division Method.
● To find the Highest Common Factor of three numbers by using Division Method.
5th Grade Numbers Page
5th Grade Math Problems
From Prime Factorisation to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
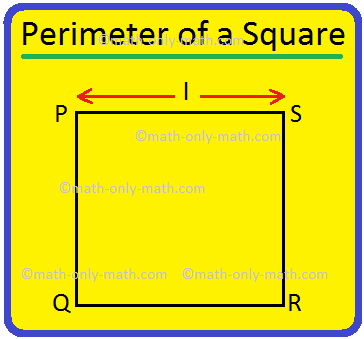
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
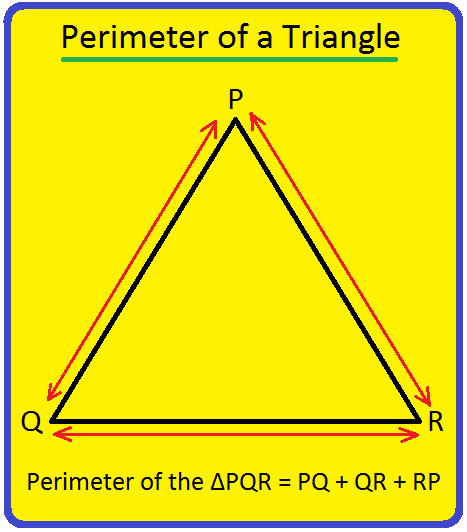
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
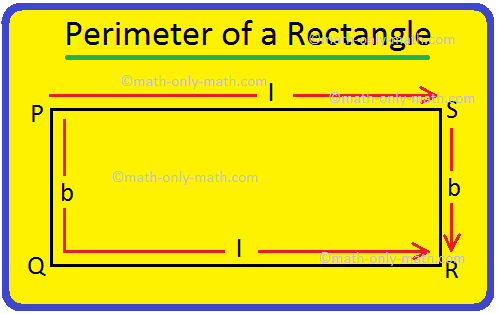
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…